题目内容
【题目】按照下面的步骤计算:
任意写一个三位数,百位数字比个数数字大3交换差的百位数字与个位数字用大数减去小数交换它的百位数字与个位数字做加法
问题:(1)用不同的三位数再做两次,结果都是1089吗?
(2)你能解释其中的道理吗?
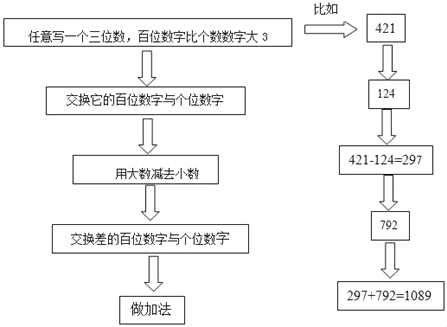
【答案】(1)结果是1089;用不同的三位数再做几次,结果都是一样的;(2)见解析.
【解析】
设这个三位数为100(3+c)+10b+c,再交换百位数字与个位数字后为100c+10b+3+c.再根据条件推理,可得结果是1089.
解:(1)结果是1089;用不同的三位数再做几次,结果都是一样的;
(2)设这个三位数为100(3+c)+10b+c,再交换百位数字与个位数字后为100c+10b+3+c.
根据题意,有[100(3+c)+10b+c]﹣[100c+10b+3+c]=297.
再交换297的百位和个位数字得792,而297+792=1089.
所以用不同的三位数再做几次,结果都是1089.

练习册系列答案
相关题目
【题目】甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 87 | 95 | 85 | 93 |
乙 | 80 | 80 | 90 | 90 |
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定