题目内容
【题目】在平面直角坐标系中,已知点![]() ,
,![]() 与坐标原点O在同一直线上,且AO=BO,其中m,n满足
与坐标原点O在同一直线上,且AO=BO,其中m,n满足![]() .
.
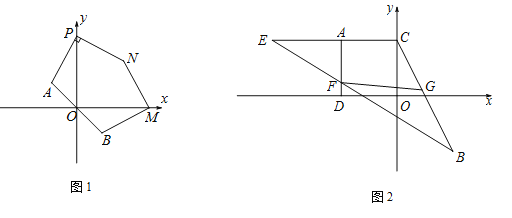
(1)求点A,B的坐标;
(2)如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且![]() ,PA⊥PN,
,PA⊥PN,![]() ,求证:BM⊥MN;
,求证:BM⊥MN;
(3)如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使![]() ,连结BE交AD于点F,恰好有
,连结BE交AD于点F,恰好有![]() ,点G是CB上一点,且
,点G是CB上一点,且![]() ,连结FG,求证:
,连结FG,求证:![]() .
.
【答案】(1)A点坐标为(-1,1),B点坐标为(1,-1);(2)详见解析;(3)详见解析.
【解析】
(1)将关于m、n的关系式进行变形,成为连个完全平方式的和,解出m和n的值,即可得到A、B的坐标.
(2)求证两线段垂直,可以通过将两直线所成的角进行拆分,然后计算各个角相加的和,本题通过在x轴负半轴取点Q,OQ=OM,连接QA,QP,PM,然后根据题干中条件和辅助线条件求证 △PQA≌△PMN,得出PQ=PM,再继续求证△PQA≌△PMN,得到△QPM为等腰直角三角形,得出角PQM=45°,再根据等量代换,求∠NMP、∠OMB、∠QMP之和即可.
(3)要求证![]() ,只需证两边所在三角形全等即可,即求证△EFH≌△FBG.根据点的坐标特征和等量代换关系得出
,只需证两边所在三角形全等即可,即求证△EFH≌△FBG.根据点的坐标特征和等量代换关系得出![]() ,然后求证
,然后求证![]() ,根据三角形全等的性质得到和等量代换得到
,根据三角形全等的性质得到和等量代换得到![]() ∠FBG=∠EHF,最后根据三角形全等的判定方法证明△EFH≌△FBG即可解决.
∠FBG=∠EHF,最后根据三角形全等的判定方法证明△EFH≌△FBG即可解决.
(1)解:∵![]()
∴![]()
即![]()
∴![]()
解得:![]()
∵![]() ,
,![]()
∴A点坐标为(-1,1),B点坐标为(1,-1)
(2)证明:

如图,在x轴负半轴取点Q,OQ=OM,连接QA,QP,PM,
∵AO=BO,∠AOQ=∠BOM
∴△AOQ≌△BOM(SAS)
∠AQO=∠BMO
∴AQ=BM=MN,
又∵OQ=OM,PO⊥QM
∴PQ=PM,
又∵PA=PN
∴△PQA≌△PMN(SSS)
∴∠QPA=∠MPN,∠PQA=∠PMN
∴∠QPA+∠APM=∠MPN+∠APM=90°
∴△QPM为等腰直角三角形
∴∠PMQ=∠PQM=45°,
∵∠PQA=∠NMP,∠AQO=∠OMB
∴∠PQA+∠AQO=∠NMP+∠OMB=∠PQM=45°
∴∠NMP+∠OMB+∠QMP=90°.
∴BM⊥MN
(3)证明:过B作BH⊥AF交AF延长线于H,连接EH,如图:

∵点A的坐标为(-1,1),点B的坐标为(1,-1)
∴H点的坐标为(-1,-1)
∴![]()
又∵CG=1,
![]()
∵AC⊥y轴,AD⊥x轴,BH⊥AH
∴∠FHB=∠EAH,
![]()
![]() ∠EHA=∠FBH
∠EHA=∠FBH
∵AE=BG,AC=CG,
∴CE=CB
∴∠CEB=∠CBE
又∵∠HBE=∠CEB
∴∠HBE=∠EBC
∴∠FBG=∠EHF
在△EFH和△FBG中

∴△EFH≌△FBG
![]()

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案




