题目内容
【题目】如图,![]() ,四边形ABCD的顶点A在
,四边形ABCD的顶点A在![]() 的内部,B,C两点在OM上(C在B,O之间),且
的内部,B,C两点在OM上(C在B,O之间),且![]() ,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是__________.
,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是__________.

【答案】2
【解析】
根据最短路径的解决方法,分别作A点关于OM和ON的对称点,通过连接对称点,列出四边形周长的公式,根据题目已知条件,要使四边形ABCD的周长最短,只需使四点共线即可,然后根据三角形内角和和锐角三角函数计算求解即可.

分别过射线ON、射线OM作点A的对称点![]() ,连接
,连接![]() ,过点
,过点![]() 作CD的垂线垂足为
作CD的垂线垂足为![]() ,连接
,连接![]() C,由图可知,AQ=
C,由图可知,AQ=![]() Q=
Q=![]() C,AB>AQ,当A、B、
C,AB>AQ,当A、B、![]() 共线时,AB最短,
共线时,AB最短,![]() C=AB,∵四边形ABCD周长=AB+BC+CD+DA=
C=AB,∵四边形ABCD周长=AB+BC+CD+DA=![]()
![]()
∴当![]() 、C、D、
、C、D、![]() 四点共线时,四边形ABCD的周长最短
四点共线时,四边形ABCD的周长最短
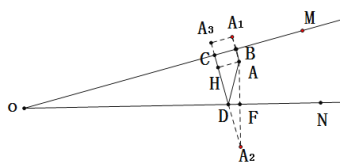
∵∠MON=15°,CD垂直OM
∴∠ODC=90°-15°=75°
∴![]() =75°
=75°
∵A点和![]() 点关于OM对称
点关于OM对称
∴∠ADF=75°
∴∠BDH=180°-75°-75°=30°
过A点作CD的垂线,垂足为H
∵BC=1
∴AH=1
在Rt△BHD中,
AD=![]()
故答案为:2

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目