题目内容
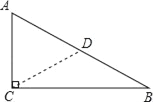
【题目】如图，在Rt△ABC中，∠C=90°，AC=
AB．求证：∠B=30°．
请填空完成下列证明．
证明：如图，作Rt△ABC的斜边上的中线CD，
则 CD=AB=AD （ ）．
∵AC=AB，
∴AC=CD=AD 即△ACD是等边三角形．
∴∠A= °．
∴∠B=90°﹣∠A=30°．
【答案】直角三角形斜边上的中线等于斜边的一半；60．
【解析】
根据直角三角形斜边上的中线等于斜边的一半和等边三角形的判定与性质填空即可．
证明：如图，作Rt△ABC的斜边上的中线CD，
则CD=
AB=AD（直角三角形斜边上的中线等于斜边的一半），
∵AC=AB，
∴AC=CD=AD 即△ACD是等边三角形，
∴∠A=60°，
∴∠B=90°﹣∠A=30°．
练习册系列答案
阅读快车系列答案
相关题目
