题目内容
【题目】(新定义):A、B、C 为数轴上三点,若点 C 到 A 的距离是点 C 到 B 的距离的 3 倍,我们就称点
C 是(A,B)的幸运点.
(特例感知):
(1)如图 1,点 A 表示的数为﹣1,点 B 表示的数为 3.表示 2 的点 C 到点 A 的距离是 3, 到点 B 的距离是 1,那么点 C 是(A,B)的幸运点.
①(B,A)的幸运点表示的数是 ;A.﹣1; B.0; C.1; D.2
②试说明 A 是(C,E)的幸运点.
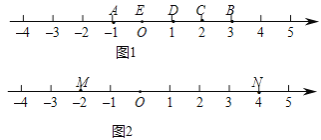
(2)如图 2,M、N 为数轴上两点,点 M 所表示的数为﹣2,点 N 所表示的数为 4,则(M,N)的幸点示的数为 .
(拓展应用):
(3)如图 3,A、B 为数轴上两点,点 A 所表示的数为﹣20,点 B 所表示的数为 40.现有一只电子蚂蚁 P 从点 B 出发,以 3 个单位每秒的速度向左运动,到达点 A 停止.当 t 为何值时,P、A 和 B 三个点中恰好有一个点为其余两点的幸运点?

【答案】(1)①B,②见详解;(2)7或2.5;(3)t为5秒,15秒,![]() 秒,
秒,![]() 秒.
秒.
【解析】
(1)①由题意可知,点0到B是到A点距离的3倍;②由数轴可知,AC=3,AE=1,可得AC=3AE;
(2)设【M,N】的幸运点为P,T表示的数为p,由题意可得|p+2|=3|p-4|,求解即可;
(3)由题意可得,BP=3t,AP=60-3t,分四种情况讨论:①当P是【A,B】的幸运点时,PA=3PB②当P是【B,A】的幸运点时,PB=3PA③当A是【B,P】的幸运点时,AB=3PA,④当B是【A,P】的幸运点时,AB=3PB.
解:(1)①由题意可知,点0到B是到A点距离的3倍,
即EA=1,EB=3,
故选B.
②由数轴可知,AC=3,AE=1,
∴AC=3AE,
∴A是【C,E】的幸运点.
(2)设【M,N】的幸运点为P,T表示的数为p,
∴PM=3PN,
∴|p+2|=3|p-4|,
∴p+2=3(p-4)或p+2=-3(p-4),
∴p=7或p=2.5;
故答案为7或2.5;
(3)由题意可得,BP=3t,AP=60-3t,
①当P是【A,B】的幸运点时,PA=3PB,
∴60-3t=3×3t,
∴t=5;
②当P是【B,A】的幸运点时,PB=3PA,
∴3t=3×(60-3t),
∴t=15;
③当A是【B,P】的幸运点时,AB=3PA,
∴60=3(60-3t)
∴t=![]() ;
;
④当B是【A,P】的幸运点时,AB=3PB,
∴60=3×3t,
∴t=![]() ;
;
∴t为5秒,15秒,![]() 秒,
秒,![]() 秒时,P、A、B中恰好有一个点为其余两点的幸运点.
秒时,P、A、B中恰好有一个点为其余两点的幸运点.