题目内容
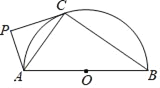
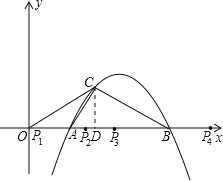
【题目】已知抛物线y=ax2﹣8ax+12a（a＜0）与x轴交于A、B两点(点A在点B的左边)，抛物线上另有一点C在第一象限，且使△OCA∽△OBC，
（1）求OC的长及
的值；
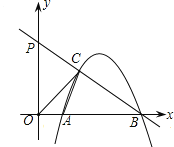
（2）设直线BC与y轴交于P点，当点C恰好在OP的垂直平分线上时，求直线BP和抛物线的解析式．
【答案】（1）2
， （2）
【解析】
分析: （1）令抛物线中y=0，可得出A、B的坐标，即可确定OA，OB的长．根据△OCA∽△OBC，可得出关于OC、OA、OB的比例关系式即可求出OC的长．
（2）利用相似三角形的对应边成比例和勾股定理来求C点的坐标．将C点坐标代入抛物线中即可求出抛物线的解析式．
详解:
（1）由ax2-8ax+12a=0（a＜0）
得x1=2，x2=6．
即：OA=2，OB=6．
∵△OCA∽△OBC，
∴OC2=OAOB=2×6．
∴OC=2（-2舍去）．
∴线段OC的长为2．
.
（2）由题意得C是BP的中点，
∴OC=BC从而C点的横坐标为3
又
,
∴
.
设直线BP的解析式为y=kx+b，过点B（6，0），，
则有
∴
∴
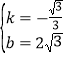
又点在抛物线上∴
，
∴
.
∴抛物线解析式为：．
点睛: 本题考查了二次函数的知识，其中涉及了数形结合问题，由抛物线求二次函数的解析式，用几何中相似三角形的性质求点的坐标等知识．注意这些知识的综合应用.
练习册系列答案
相关题目
