��Ŀ����
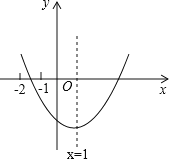
����Ŀ����֪OΪ����ԭ�㣬������y1=ax2+bx+c��a��0����x���ཻ�ڵ�A��x1��0����B��x2��0������y�ύ�ڵ�C����O��C�����ľ���Ϊ3��x1x2��0��|x1|+|x2|=4����A��C��ֱ��y2=��3x+t�ϣ�
��1����y1����x�����������ʱ�����Ա���x��ȡֵ��Χ��
��2����������y1����ƽ��n��n��0������λ����ƽ�ƺ�y����x�����������IJ���ΪP��ֱ��y2����ƽ��n����λ����ƽ�ƺ��ֱ����P�й�����ʱ����2n2��5n����Сֵ��
���𰸡���1����c=3����y��x���������ʱ��x�ܩ�1����c=��3����y��x���������ʱ��x��1����2����n=![]() ʱ��2n2��5n����СֵΪ��
ʱ��2n2��5n����СֵΪ��![]() ��
��
��������
��1���ֱ����â���C��0��3������c=3���Լ�����C��0��-3������c=-3���ó�A��B�����꣬���������������ʽ�������ó��𰸣�
��2�����â���c=3����y1=-x2-2x+3=-��x+1��2+4��y2=-3x+3���ó�y1����ƽ��n����λ�������ʽΪ��y3=-��x+1+n��2+4���������ƽ�ƺ��ֱ����P�й�����ʱ�ó�n��ȡֵ��Χ������c=-3����y1=x2-2x-3=��x-1��2-4��y2=-3x-3��y1����ƽ��n����λ�������ʽΪ��y3=��x-1+n��2-4���������ƽ�ƺ��ֱ����P�й�����ʱ�ó�n��ȡֵ��Χ�����������䷽�����������ֵ��
��1����x1x2��0��
��x1��x2��ţ�
����C��0��3������c=3��
��C��0��3������y2=��3x+t����0+t=3����t=3��
��y2=��3x+3��
��A��x1��0������y2=��3x+3����3x1+3=0��
��x1=1��
��A��1��0����
��x1��x2��ţ�x1=1��0����x2��0��
��|x1|+|x2|=4��
��1��x2=4��
��ã�x2=��3����B����3��0����
����y1=ax2+bx+3�ã�![]() ��
��
��ã�![]() ��
��
��y1=��x2��2x+3=����x+1��2+4��
��x�ܩ�1ʱ��y��x���������
����C��0����3������c=��3��
��C��0����3������y2=��3x+t����0+t=��3����t=��3��
��y2=��3x��3��
��A��x1��0��������y2=��3x��3��
��3x1��3=0��
��x1=��1��
��A����1��0����
��x1��x2��ţ�x1=��1��0����x2��0
��|x1|+|x2|=4��
��1+x2=4��
��ã�x2=3����B��3��0����
����y1=ax2+bx+3�ã�![]() ��
��
��ã�![]() ��
��
��y1=x2��2x��3=��x��1��2��4��
��x��1ʱ��y��x���������
������������c=3����y��x���������ʱ��x�ܩ�1��
��c=��3����y��x���������ʱ��x��1��
��2������c=3����y1=��x2��2x+3=����x+1��2+4��y2=��3x+3��
y1����ƽ��n����λ�������ʽΪ��y3=����x+1+n��2+4��
��x�ܩ�1��nʱ��y��x���������
y2����ƽ��n����λ�������ʽΪ��y4=��3x+3��n��
Ҫʹƽ�ƺ�ֱ����P�й����㣬��x=��1��n��y3��y4��
��������1��n+1+n��2+4�ݩ�3����1��n��+3��n��
��ã�n�ܩ�1��
��n��0����n�ܩ�1������������Ӧ��ȥ��
����c=��3����y1=x2��2x��3=��x��1��2��4��y2=��3x��3��
y1����ƽ��n����λ�������ʽΪ��y3=��x��1+n��2��4��
��x��1��nʱ��y��x���������
y2����ƽ��n����λ�������ʽΪ��y4=��3x��3��n��
Ҫʹƽ�ƺ�ֱ����P�й����㣬��x=1��n��y3��y4��
����1��n��1+n��2��4�ܩ�3��1��n����3��n��
��ã�n��1��
����������n��1��
2n2��5n=2��n��![]() ��2��
��2��![]() ��
��
�൱n=![]() ʱ��2n2��5n����СֵΪ����
ʱ��2n2��5n����СֵΪ����![]() ��
��

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�