��Ŀ����
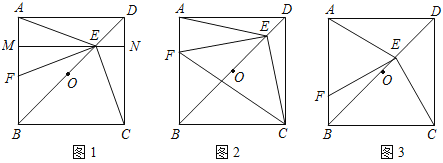
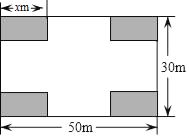
����Ŀ��ijС��ҵ��ίԱ�������һ�鳤50m����30m�ľ��οյؽ��ɽ����㳡����Ʒ�����ͼ��ʾ����Ӱ����Ϊ�̻������Ŀ��̻���Ϊȫ�ȵľ��Σ����հ�����Ϊ����������ܵ�4�����ڿ�����ͬ������Ȳ�С��14m��������26m�����̻����ϳ���Ϊxm����������Ϊym2
��1��ֱ��д��������x��ʽ�ӱ�ʾ���ڵĿ���Ϊ�� ����
��y��x�ĺ�����ϵʽ��x��ȡֵ��Χ�� ����
��2�����������y����������
��3��Ԥ�ƻ�����Ϊ50Ԫ/m2���̻������Ϊ40Ԫ/m2�����ҵ��ίԱ��Ͷ�ʲ��ó���72000Ԫ�����뽨�죬��xΪ����ʱ�����м��ֽ��췽����
���𰸡���1����50��2x����y����4x2+40x+1500��12��x��18������2��1404m2����3������4�ֽ��췽����
��������
��1���پ��εij���ȥ�����̻����ϳ��������.
��y=��������-4���̻������������![]() �ó�x�ķ�Χ.
�ó�x�ķ�Χ.
��2����y����4x2+40x+1500����Ϊ����ʽ��4��x��5��2+1600���������������ʼ������.
��3�������Ϊw���������w����40��x��5��2+76000���������������ʺ�x��ȡֵ��Χ��ϼ������.
�⣺��1���ٳ��ڵĿ���Ϊ��50��2x��
�ڸ�������ã�y��50��30��4x��x��10����
��y��x�ĺ�����ϵʽ��x��ȡֵ��ΧΪ��y����4x2+40x+1500��12��x��18����
�ʴ�Ϊ��50��2x��y����4x2+40x+1500��12��x��18����
��2��y����4x2+40x+1500����4��x��5��2+1600��
��a����4��0�������ߵĿ������£��Գ���Ϊx��5����12��x��18ʱ��y��x���������С��
�൱x��12ʱ��y�����1404��
�𣺻�������y��������Ϊ1404m2��
��3�������Ϊw��
������ã�w��50����4x2+40x+1500��+40��4x��x��10������40��x��5��2+76000��
�൱w��72000ʱ����ã�x1����5��x2��15��
��a����40��0��
�൱x����5��x��15ʱ��w��72000��
��12��x��18��
��15��x��18����x������
���4�ֽ��췽����