Question

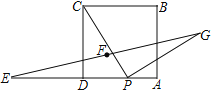
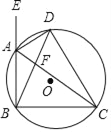
【题目】已知：如图，AD是△ABC的外角∠EAC的平分线，与△ABC的外接圆交于点D，AC与BD相交于点F．

（1）求证：DB＝DC；

（2）若DA＝DF，求证：△BCF∽△BDC．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）根据圆内接四边形的性质可证∠EAD=∠DCB，再根据圆周角定理可证∠DAC=∠DBC，又已知∠EAD=∠DAC，即∠DCB=∠DBC得证，再根据等角对等边即可得证．
（2）先根据DA＝DF得出∠DAF＝∠DFA，再根据圆周角定理∠DAF＝∠FBC，对顶角∠DFA＝∠BFC，得出∠FBC＝∠BFC，再根据相似三角形的判定解答即可．

证明：（1）∵AD是∠EAC的平分线，

∴∠EAD＝∠DAC，

∵∠EAD是圆内接四边形ABCD的外角，

∴∠EAD＝∠DCB（圆内接四边形外角等于内对角），

又∵∠DAC＝∠DBC，

∴∠DCB＝∠DBC，

∴DB＝DC；

（2）∵DA＝DF，

∴∠DAF＝∠DFA，

∵∠DAF＝∠FBC，∠DFA＝∠BFC，

∴∠FBC＝∠BFC，

∵∠DCB＝∠DBC，

∴∠DCB＝∠BFC，而∠FBC＝∠DBC，

∴△BCF∽△BDC．