题目内容
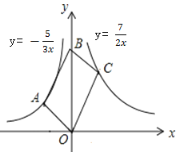
【题目】如图,在平面直角坐标系中,直线![]() 分别交两坐标轴于A、B两点,直线y=-2x+2分别交两坐标轴于C、D两点
分别交两坐标轴于A、B两点,直线y=-2x+2分别交两坐标轴于C、D两点
(1)求A、B、C、D四点的坐标
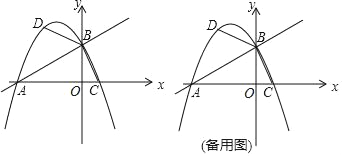
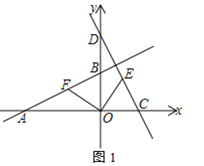
(2)如图1,点E为直线CD上一动点,OF⊥OE交直线AB于点F,求证:OE=OF
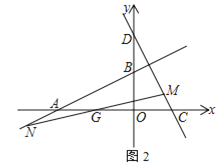
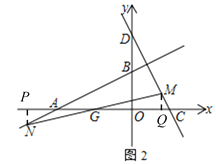
(3)如图2,直线y=kx+k交x轴于点G,分别交直线AB、CD于N、M两点.若GM=GN,求k的值
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)分别针对于直线AB. CD的解析式,令x=0和y=0, 解方程即可得出结论;
(2)先判断出AO=OD,OB=OC,得出△AOB≌△DOC (SAS) 。进而得出∠OAB=∠ODC,再利用同角的余角相等判断出∠AOF=∠BOE,得出△AOF≌△DOE (ASA),即可得出结论;
(3)先求出点G的坐标,设出点M、N的坐标,利用中点坐标公式建立方程组求解得出m,n,进而得出点M坐标,代入直线y=kx+k中,即可得出结论.
解:(1)∵![]()
∴令x=0,则y=1.
∴B(0,1)
∵![]()
令y=0, 则![]() ,
,
∴x=-2,
∴A(-2, 0)
∵![]()
令x=0,则y=2,
∴D(0,2),
∵![]()
令y=0,则-2x+2=0,
∴x=1 ,
∴C(1.0)
(2)由(1)知,A(-2,0),B(0,1),C(1,0),D(0,2),
∴OA=2,OB=1,OC=1,OD=2
∴![]() ,
,![]()
又∵∠AOB=∠DOC
∴![]()
∴∠OAB=∠ODC
∵![]()
∴∠BOF+∠BOE=90°
∵∠BOF+∠AOF=90°
∴![]()
∴![]()
∴![]()
(3)∵![]()
∴必过![]() 轴上一定点
轴上一定点![]()
分别作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]()
∵![]() ,
,
∴![]()
∴![]() ,
,![]()
设![]()
∴![]()
∴![]()
∴![]() 即
即![]() ,
,![]()
∴![]() 的解析式为
的解析式为![]()
∴![]()

练习册系列答案
相关题目