Question

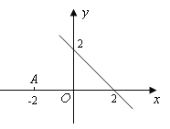
【题目】已知抛物线与轴交于，两点，且，两点均在直线的下方，那么下列说法正确的是（ ）

A.抛物线开口一定向上B.抛物线的顶点不可能在第四象限

C.抛物线与已知直线有两个交点D.抛物线的对称轴可能在轴右侧

Answer 1

【答案】B

【解析】

结合二次函数与一次函数的图象，以及二次函数的图象性质对四个选项逐一判断即可；

因为直线与轴交于点，与轴交于点，且抛物线与轴交于，两点，且，两点均在直线的下方，由于点在直线下方的位置不确定，可能在点的右侧，也可能在点的左侧，因此，抛物线的开口不能确定，故A错误；且当抛物线开口向下时，与已知直线可能没有交点，故C错误；根据抛物线的对称性，点只能在的左侧，故抛物线的对称轴不可能在轴右侧，且抛物线的顶点不可能在第四象限，故D错误，B正确．

故选：B.