题目内容
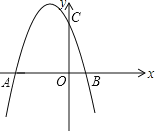
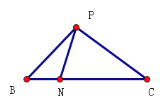
【题目】如图，
中，
，
，
，
为半圆
的直径，将沿射线
方向平移得到△A1B1C1．当
与半圆相切于点
时，平移的距离的长为__________．
【答案】
【解析】
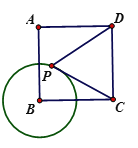
如图，连接OD，根据切线性质可得∠ODB1=90°，根据平移的性质可得∠B1=∠ABC，利用勾股定理可求出BC的长，即可求出半圆的半径，利用∠B1的正弦即可求出OB1的长，即可求出平移距离BB1的长．
如图，连接OD，
∵
，
，
，
∴BC=
=4，
∵BC为半圆
的直径，
∴OD=OB=
BC=2，
∵半圆相切于点
，
∴OD⊥A1B1，
∵将
沿射线
方向平移得到△A1B1C1，
∴∠B1=∠ABC，
∴sin∠B1=sin∠ABC=
=
，
∴OB1=
=
，
∴BB1=OB1-OB=-2=，即平移的距离的长为．
故答案为：
练习册系列答案
文敬图书课时先锋系列答案
相关题目
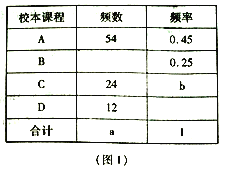
【题目】如下表，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中仼意三个相邻格子中所填整数之和都相等．
|
|
|
| 5 | 4 | …… |
（1）可求得
_____；
_____；
_____．
（2）第2019个格子中的数为______；
（3）前2020个格子中所填整数之和为______．
（4）前
个格子中所填整数之和是否可能为2020？若能，求出的值，若不能，请说明理由．
