题目内容
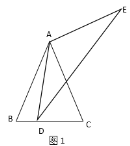
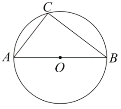
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,点
上,点![]() 是
是![]() 上一动点,且与点
上一动点,且与点![]() 分别位于直径
分别位于直径![]() 的两侧,
的两侧,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ;
;

(1)当点![]() 运动到什么位置时,
运动到什么位置时,![]() 恰好是
恰好是![]() 的切线?画出图形并加以说明.
的切线?画出图形并加以说明.
(2)若点![]() 与点
与点![]() 关于直径
关于直径![]() 对称,且
对称,且![]() ,画出图形求此时
,画出图形求此时![]() 的长.
的长.
【答案】(1)画图见解析,证明见解析;(2)画图见解析,CQ=6.4.
【解析】
(1)画出图形,根据切线的判定,直接判断即可;
(2)画出图形,根据tan∠CPB=tanA=![]() ,AB=5,求出AC,BC的长,再根据对称,利用等积法求出CP的长度,最后,再根据tan∠CPB=
,AB=5,求出AC,BC的长,再根据对称,利用等积法求出CP的长度,最后,再根据tan∠CPB=![]() =
=![]() ,求出CQ的长即可.
,求出CQ的长即可.
解:(1)当点P运动到直线OC与⊙O的交点处.

如图,当点P运动到直线OC与⊙O的交点处时,则CP为![]() 的直径,
的直径,
又∵![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
(2)如图,连接CB.
∵AB是直径,
∴∠ACB=90°,
∵∠P=∠A,
∴tan∠CPB=tanA=![]() ,
,
在Rt△ABC中,tanA=![]() ,
,
∴设BC=4k,则AC=3k,
又∵AB=5,
∴(4k)2+(3k)2=52,
∴k=1(舍负)
∴AC=3,BC=4.
∵点P与点C关于直径AB对称,
∴CP⊥AB,
在Rt△ABC中,CP=![]() =4.8,
=4.8,
在Rt△PCQ中,tan∠CPB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴CQ=6.4.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目