��Ŀ����
����Ŀ���ۺ���ʵ��
�����龳
���ۺ���ʵ�����ϣ�ͬѧ�����������ε��۵���Ϊ���չ��ѧ���
��������
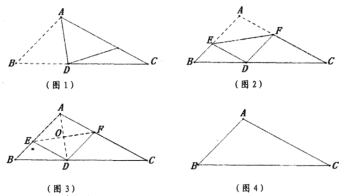
�������С���ͬѧ��һ�Ŷ۽�������ֽƬ![]() ��
��![]() Ϊ�۽ǣ����������²�����
Ϊ�۽ǣ����������²�����
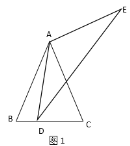
��һ������ͼ1���۳�![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ��
��
�ڶ�������ͼ2��չƽֽƬ���ٴ��۵���������ֽƬ��ʹԤ��![]() ���
���![]() �غϣ����
�غϣ����![]() �ֱ���
�ֱ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��
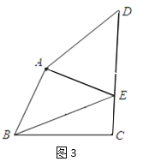
����������ͼ3���ٴ�չƽֽƬ������![]() ��
��![]() ���ɵ��ı���
���ɵ��ı���![]() ��
��
��1����ͼ4��![]() �����ó߹������ۺ�
�����ó߹������ۺ�![]() ��
��![]() ��
��
��Ҫ������ͼ�ۼ�����д������
ʵ��̽��
��2�����ж�ͼ3���ı���![]() ����״����д��֤�����̣�
����״����д��֤�����̣�
����̽��
��3�����¾�����С���ͬѧͻ�����룬���������С��ͬѧ�����Ļ��������������һ�����⣺��ͼ3�У�����![]() ���ֱ�
���ֱ�![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���������������ε�֪ʶ�������
���������������ε�֪ʶ�������![]() �ij�������д�������̣�
�ij�������д�������̣�
���𰸡���1������������2�����Σ�֤������������3��![]() �����̼�����
�����̼�����
��������
��1������BAC�Ľ�ƽ����AD��BC���ڵ�D������AD���д�����AB����E����AC����F���ɣ�
��2�����۵���֪��![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ��
��![]() �Ĵ�ֱƽ���ߣ���ͨ����ֱƽ���ߺͽ�ƽ���ߵ����ʿɵ�
�Ĵ�ֱƽ���ߣ���ͨ����ֱƽ���ߺͽ�ƽ���ߵ����ʿɵ�![]() ��
��![]() ������֤���ı���
������֤���ı���![]() ��ƽ���ı��Σ��ٸ���
��ƽ���ı��Σ��ٸ���![]() ����֤ƽ���ı���
����֤ƽ���ı���![]() �����Σ�
������
��3������![]() ��ͨ��֤��
��ͨ��֤��![]() ���ɵ�
���ɵ�![]() ����
����![]() �����
�����![]() ���Ӷ��ó�
���Ӷ��ó�![]() ��
��
�⣺��1����ͼ��ʾ��
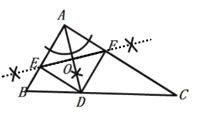
��2������
֤�������۵���֪��![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ��
��![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����
��![]() ��
��![]() ��
��
��![]() ��
��![]()
��![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����
��![]()
��![]() ��
��![]()
��![]() ��
��![]()
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�֡�![]()
��ƽ���ı���![]() �����Σ�
������
��3������![]() ��
��
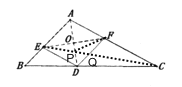
���ı���![]() Ϊ���Σ�
����
��![]() ��ֱƽ��
��ֱƽ��![]() ��
��
���![]() ��
��![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() �ϣ�
�ϣ�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�����Ŀ�����±�������ߵ�һ�����ӿ�ʼ����������ÿ��С�����ж�����һ��������ʹ�����Ё����������ڸ�������������֮�Ͷ���ȣ�
|
|
|
| 5 | 4 | ���� |
��1�������![]() _____��
_____��![]() _____��
_____��![]() _____��
_____��
��2����2019�������е���Ϊ______��
��3��ǰ2020����������������֮��Ϊ______��
��4��ǰ![]() ����������������֮���Ƿ����Ϊ2020�����ܣ����
����������������֮���Ƿ����Ϊ2020�����ܣ����![]() ��ֵ�������ܣ���˵�����ɣ�
��ֵ�������ܣ���˵�����ɣ�