题目内容
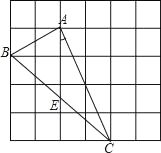
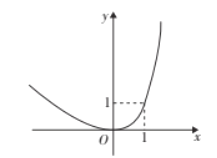
【题目】对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如:下图中的函数有0,1两个不变值,其不变长度q等于1.
(1)分别判断函数y=x-1,y=x-1,y=x2有没有不变值?如果有,直接写出其不变长度;
(2)函数y=2x2-bx.
①若其不变长度为零,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3) 记函数y=x2-2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,函数G的图象由G1和G2两部分组成,若其不变长度q满足0≤q≤3,则m的取值范围为 .
【答案】详见解析.
【解析】试题分析:(1)根据定义分别求解即可求得答案;
(2)①首先由函数y=2x2﹣bx=x,求得x(2x﹣b﹣1)=0,然后由其不变长度为零,求得答案;
②由①,利用1≤b≤3,可求得其不变长度q的取值范围;
(3)由记函数y=x2﹣2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,可得函数G的图象关于x=m对称,然后根据定义分别求得函数的不变值,再分类讨论即可求得答案.
试题解析:解:(1)∵函数y=x﹣1,令y=x,则x﹣1=x,无解;
∴函数y=x﹣1没有不变值;
∵y=x-1 =![]() ,令y=x,则
,令y=x,则![]() ,解得:x=±1,∴函数
,解得:x=±1,∴函数![]() 的不变值为±1,q=1﹣(﹣1)=2.∵函数y=x2,令y=x,则x=x2,解得:x1=0,x2=1,∴函数y=x2的不变值为:0或1,q=1﹣0=1;
的不变值为±1,q=1﹣(﹣1)=2.∵函数y=x2,令y=x,则x=x2,解得:x1=0,x2=1,∴函数y=x2的不变值为:0或1,q=1﹣0=1;
(2)①函数y=2x2﹣bx,令y=x,则x=2x2﹣bx,整理得:x(2x﹣b﹣1)=0.∵q=0,∴x=0且2x﹣b﹣1=0,解得:b=﹣1;
②由①知:x(2x﹣b﹣1)=0,∴x=0或2x﹣b﹣1=0,解得:x1=0,x2=![]() .∵1≤b≤3,∴1≤x2≤2,∴1﹣0≤q≤2﹣0,∴1≤q≤2;
.∵1≤b≤3,∴1≤x2≤2,∴1﹣0≤q≤2﹣0,∴1≤q≤2;
(3)∵记函数y=x2﹣2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,∴函数G的图象关于x=m对称,∴G:y=![]() .∵当x2﹣2x=x时,x3=0,x4=3;
.∵当x2﹣2x=x时,x3=0,x4=3;
当(2m﹣x)2﹣2(2m﹣x)=x时,△=1+8m,当△<0,即m<﹣![]() 时,q=x4﹣x3=3;
时,q=x4﹣x3=3;
当△≥0,即m≥﹣![]() 时,x5=
时,x5=![]() ,x6=
,x6=![]() .
.
①当﹣![]() ≤m≤0时,x3=0,x4=3,∴x6<0,∴x4﹣x6>3(不符合题意,舍去);
≤m≤0时,x3=0,x4=3,∴x6<0,∴x4﹣x6>3(不符合题意,舍去);
②∵当x5=x4时,m=1,当x6=x3时,m=3;
当0<m<1时,x3=0(舍去),x4=3,此时0<x5<x4,x6<0,q=x4﹣x6>3(舍去);
当1≤m≤3时,x3=0(舍去),x4=3,此时0<x5<x4,x6>0,q=x4﹣x6<3;
当m>3时,x3=0(舍去),x4=3(舍去),此时x5>3,x6<0,q=x5﹣x6>3(舍去);
综上所述:m的取值范围为1≤m≤3或m<﹣![]() .
.

 名校课堂系列答案
名校课堂系列答案