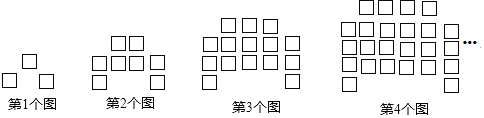
题目内容
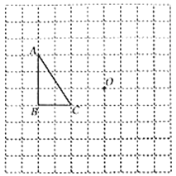
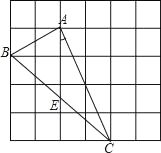
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
【答案】(1)作图见解析;(2)![]() ;(3)∠CAD;
;(3)∠CAD;![]() ;或∠ADC,
;或∠ADC,![]() .
.
【解析】试题分析:(1)直接利用网格结合平行线的判定方法得出D点位置;
(2)直接利用勾股定理得出DC的长;
(3)利用勾股定理的逆定理得出△ACD是直角三角形,进而得出答案;
(4)根据直角三角形斜边上的中线等于斜边的一半得出AE=EC,可得∠ACB=∠CAE,然后在Rt△ABC中求出tan∠ACB的值即为tan∠CAE的值.
试题解析:
解:(1)如图所示:
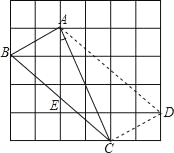
D点即为所求;
(2)DC=![]() =
=![]() ;
;
故答案为:![]() ;
;
(3)在△ACD的三个内角中所选的锐角是:∠CAD,
∵CD=![]() ,AD=5,AC=
,AD=5,AC=![]() ,
,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴∠CAD它所对应的正弦函数值是:![]() =
=![]() ;
;
当所选的锐角是:∠ADC,
则∠ADC它所对应的正弦函数值是:![]() =
=![]() .
.
故答案为:∠CAD,![]() 或∠ADC,
或∠ADC,![]() ;
;
(4)AB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
∵E为BC中点,
∴AE=EC,
∴∠ACB=∠CAE,
∴tan∠CAE=tan∠ACB=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目