题目内容
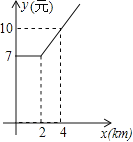
【题目】如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,甲车到达C地后因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,乙车行驶的时间t= 小时;
(2)求甲车从C地按原路原速返回A地的过程中,甲车距它出发地的路程y与它出发的时间x的函数关系式;
(3)直接写出甲车出发多长时间两车相距80千米.

【答案】(1) 乙车速度为:80千米/时,乙车行驶全程的时间6小时;(2)y=﹣120x+600;(3)甲车出发![]() 小时或3小时或
小时或3小时或![]() 两车相距80千米
两车相距80千米
【解析】
(1)结合题意,利用速度=路程÷时间,可得乙的速度、行驶时间;
(2)找到甲车到达C地和返回A地时x与y的对应值,利用待定系数法可求出函数解析式;
(3)甲、乙两车相距80千米有两种情况:
①相向而行:相等关系为“甲车行驶路程+乙车行驶路程+甲乙间距离=480”,
②同向而行:相等关系为“甲车距它出发地的路程+乙车路程﹣甲乙间距离=480”
分别根据相等关系列方程可求解.
解:(1)∵乙车比甲车先出发1小时,由图象可知乙行驶了80千米,
∴乙车速度为:80千米/时,乙车行驶全程的时间t=480÷80=6(小时);
(2)根据题意可知甲从出发到返回A地需5小时,
∵甲车到达C地后因立即按原路原速返回A地,
∴结合函数图象可知,当x=![]() 时,y=300;当x=5时,y=0;
时,y=300;当x=5时,y=0;
设甲车从C地按原路原速返回A地时,即![]() ≤x≤5,
≤x≤5,
甲车距它出发地的路程y与它出发的时间x的函数关系式为:y=kx+b,
将![]() 函数关系式得:
函数关系式得: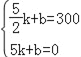 ,
,
解得:![]() ,
,
故甲车从C地按原路原速返回A地时,
甲车距它出发地的路程y与它出发的时间x的函数关系式为:y=﹣120x+600;
(3)由题意可知甲车的速度为:![]() =120(千米/时),
=120(千米/时),
设甲车出发m小时两车相距80千米,有以下两种情况:
①两车相向行驶时,有:120m+80(m+1)+80=480,
解得:m=![]() ;
;
②两车同向行驶时,有:600﹣120m+80(m+1)﹣80=480,
解得:m=3;
③两车相遇之后,甲返回前,有120m+80(m+1)﹣80=480,
解得:m=![]() ;
;
∴甲车出发![]() 小时或3小时或
小时或3小时或![]() 两车相距80千米.
两车相距80千米.

 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】先填写表,通过观察后再回答问题:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | x | 1 | y | 100 | …… |
(1)表格中,x=_________,y=_________
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ≈___________
≈___________
②已知![]() ,若
,若![]() ,用含m的代数式表示b,则b=___________
,用含m的代数式表示b,则b=___________
(3)试比较![]() 与a的大小(直接写出结果)
与a的大小(直接写出结果)