题目内容
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN. 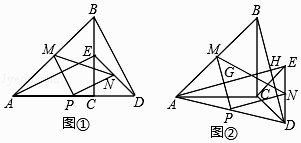
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.
【答案】
(1)证明:∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中, 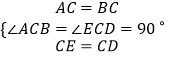 ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵∠CBD+∠BDC=90°,
∴∠EAC+∠BDC=90°,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM= ![]() BD,PN=
BD,PN= ![]() AE,
AE,
∴PM=PM,
∵PM∥BD,PN∥AE,
∴∠NPD=∠EAC,∠MPA=∠BDC,
∵∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN,
∴△PMN为等腰直角三角形
(2)解:①中的结论成立,
理由:设AE与BC交于点O,如图②所示:
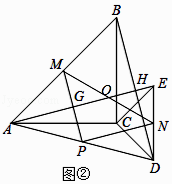
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中, 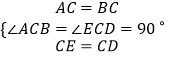 ,
,
∴△ACE≌△BCD(SAS)
∴AE=BD,∠CAE=∠CBD.
∵∠AOC=∠BOE,∠CAE=∠CBD,
∴∠BHO=∠ACO=90°,
∴AE⊥BD,
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= ![]() BD,PM∥BD,PN=
BD,PM∥BD,PN= ![]() AE,PN∥AE,
AE,PN∥AE,
∴PM=PN.
∵AE⊥BD,
∴PM⊥PN,
∴△PMN为等腰直角三角形.
【解析】(1)由等腰直角三角形的性质易证△ACE≌△BCD,由此可得AE=BD,再根据三角形中位线定理即可得到PM=PN,由平行线的性质可得PM⊥PN,于是得到结论;(2)(1)中的结论仍旧成立,由(1)中的证明思路即可证明.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了)的相关知识才是答题的关键.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案


