题目内容
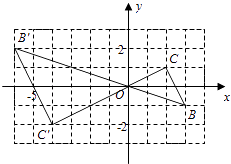
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′ , 并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
【答案】
(1) ;﹣6;2;﹣4;﹣2
;﹣6;2;﹣4;﹣2
(2)﹣2x;﹣2y
【解析】解:(1)如图
B′(﹣6,2),C′(﹣4,﹣2)
2)M′(﹣2x,﹣2y).
(1)延长BO,CO,根据相似比,在延长线上分别截取AO,BO,CO的2倍,确定所作的位似图形的关键点A',B',C'再顺次连接所作各点,即可得到放大2倍的位似图形△OB'C';再根据点的位置写出点的坐标即可;(2)M′的坐标的横坐标、纵坐标分别是M的坐标的2倍的相反数.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需 ![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需 ![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围); 表一
粗加工数量/吨 | 3 | 7 | x |
精加工数量/吨 | 47 |
表二
粗加工数量/吨 | 3 | 7 | x |
粗加工获利/元 | 2800 | ||
精加工获利/元 | 25800 |
y与x的函数关系式
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?