题目内容
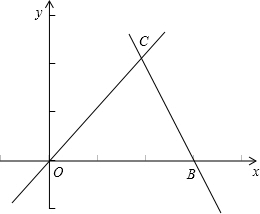 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)设△COB中位于直线m左侧部分的面积为s,求出s与x之间函数关系式.
分析:(1)联立两解析式,可求出交点坐标(2,2),根据y1>y2得出关于x的不等式,解出即可得出x的取值范围.
(2)分段表示,①0<x≤2,根据三角形的面积公式可得出s与x的关系,②2<x<3,分成两个三角形进行求解,可得出s与x的关系即可.
(2)分段表示,①0<x≤2,根据三角形的面积公式可得出s与x的关系,②2<x<3,分成两个三角形进行求解,可得出s与x的关系即可.
解答:解:(1)由题意得,x=-2x+6,
解得:x=2,即可得点C的坐标为(2,2);
∵y1>y2,即x>-2x+6,
解得:x>2;
(2)①当0<x≤2时,
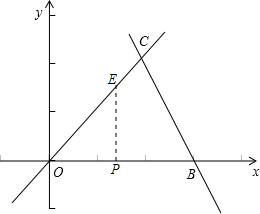
则可得OP=x,EP=x,此时s=
OP×PE=
x2;
②当2<x<3时,

过点C作CF⊥x轴于F,则S△OCF=
OF×CF=2,
S梯形EPFC=
(EP+CF)×FP=
(-2x+6+2)×(x-2)=-x2+6x-8.
故s=S△OCF+S梯形EPFC=2+(-x2+6x-8)=-x2+6x-6,
综上可得s与x的关系式为:s=
.
解得:x=2,即可得点C的坐标为(2,2);
∵y1>y2,即x>-2x+6,
解得:x>2;
(2)①当0<x≤2时,

则可得OP=x,EP=x,此时s=
| 1 |
| 2 |
| 1 |
| 2 |
②当2<x<3时,

过点C作CF⊥x轴于F,则S△OCF=
| 1 |
| 2 |
S梯形EPFC=
| 1 |
| 2 |
| 1 |
| 2 |
故s=S△OCF+S梯形EPFC=2+(-x2+6x-8)=-x2+6x-6,
综上可得s与x的关系式为:s=
|
点评:本题考查了一次函数的综合运用,难点在第二问,关键是求出点C的坐标后,分段求出s与x的关系式,不要一概而论.

练习册系列答案
相关题目
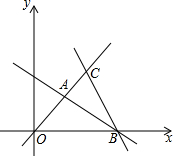 交于点A.
交于点A.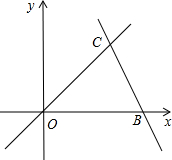 如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.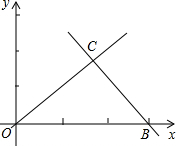 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.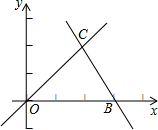 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.