题目内容
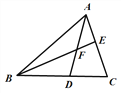
【题目】如图, ![]() ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】∵AD是△ABC的中线,
∴S△ABD=S△DCA=![]() ,故①正确;
,故①正确;
∵BE分别是是△ABC的中线,
∴S△ABE=S△BCE=![]() ,
,
∴S△ABD=S△DCA= S△ABE=S△BCE,
∴S△ABE=S△ABD,
∴S△ABE- S△ABF =S△ABD- S△ABF,
∴S△AEF=S△BDF,故②正确;
∵△ABC的中线AD、BE相交于点F,
∴S△ABF =2S△AEF.
∵S△DCA=S△ABE,
∴S△DCA- S△AEF =S△ABE- S△AEF,
∴S△ABF =S四边形EFDC,
∴S四边形EFDC=2S△AEF,故③正确;
∵△ABC的中线AD、BE相交于点F,
∴S△ABE=![]() .
.
∵S△ABC=2 S△ABE,
∴S△ABE=3 S△ABF,故④正确;
故选D.

练习册系列答案
相关题目