题目内容
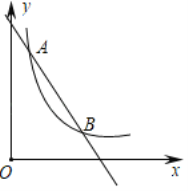
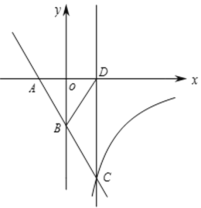
【题目】已知直线:y1=![]() 与x轴、y轴相交于A、B两点,与双曲线
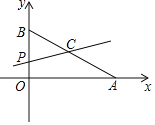
与x轴、y轴相交于A、B两点,与双曲线![]() (k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为
(k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为![]() ,且B是AC的中点.
,且B是AC的中点.
(1)求k的值;
(2)直接写出![]() 的解集;
的解集;
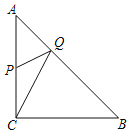
(3)若P为直线l的一动点,点P的纵坐标为m,∠APB≥30°,求m的范围.
【答案】(1)k=-2![]() ;(2)x>1;(3)-2≤m≤2.
;(2)x>1;(3)-2≤m≤2.
【解析】
(1)根据△ABD的面积为![]() 可求得OD,再根据一次函数可求得C点坐标,由此可求得k的值;
可求得OD,再根据一次函数可求得C点坐标,由此可求得k的值;
(2)将不等式进行适当变形,结合图象即可得解;
(3)以点D为圆心,AD长为半径画圆,根据圆周角定理可得∠AMB=∠ANB=30,由此求得m的取值范围.
解:(1)把x=0和y=0分别代入y1,得A(-1,0),B(0,![]() )
)
∵△ABD的面积为![]() ,
,
∴![]() ,即
,即![]() ,
,
∴AD=2,
∴OD=1
把x=1代入y1,得C(1,-2![]() ),
),
∴k= -2![]() ,
,
(2)当![]() 时
时![]() ,即
,即![]() ,
,
由图象可知:x>1;
(3)∵OA=1,OB=![]() ,
,
∴AB=2,tan∠BAO=![]() ,
,
∴∠BAO=60,AD=AB=2,
∴△ABD是等边三角形,
如图,以点D为圆心,AD长为半径画圆,与直线l交于M、N两点,
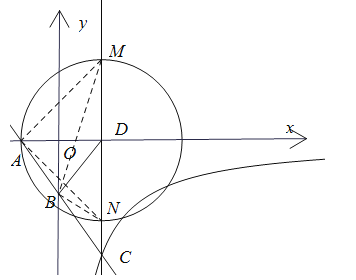
则∠AMB=∠ANB=30
当点P在线段MN上时(不同于M、N),连接AP交圆于Q,
则∠APB>∠AQB,即∠APB>30°,
当点P在线段MN外侧时,∠APB<30°,所以-2≤m≤2.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目