题目内容
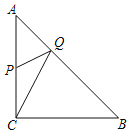
【题目】如图，在直角△ABC中，∠C＝90°，AC＝BC＝2，P为AC的中点，Q为AB上的一个动点，连接PQ，CQ，则PQ+CQ的最小值为（ ）
A.2B.3C.
D.
【答案】D
【解析】
过点P作点P关于AB的对称点P'，连接P'C，交AB点Q'，连接AP'．则AP＝AP'，PQ'＝P'Q'，当P'、Q'、C在同一直线上时，PQ＋CQ的最小值为CP'．由勾股定理得，CP'＝
=
=
，即PQ＋CQ的最小值为 .
如图，过点P作点P关于AB的对称点P'，连接P'C，交AB点Q'，连接AP'，
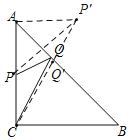
则AP＝AP'，PQ'＝P'Q'，
PQ+CQ＝P'Q+CQ
P'Q'+CQ'＝CP'，
即当P'、Q'、C在同一直线上时，PQ+CQ的最小值为CP'．
∵直角△ABC中，∠C＝90°，
∴∠CAB＝45°，∠P'AC＝45°，
∴∠CAP'＝90°，
∵AC＝BC＝2，P为AC的中点，
∴AP'＝AP＝1，
∴CP'＝==，
即PQ＋CQ的最小值为.
故选：D．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
【题目】我们把图1称为一个基本图形，显然这个基本图形中有6个矩形，将此基本图形不断复制并向上平移、叠加，这样得到图2，图3…（如图所示）
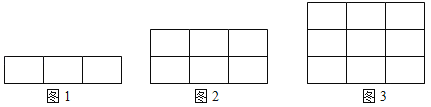
（1）观察图形，完成如表：
图形名称 | 矩形个数 |
图1 | 6 |
图2 | 18 |
图3 | 36 |
图4 | 60 |
图5 |
|
（2）根据以上规律猜想，图形n中共有多少个矩形（用含n的代数式表示）？
