题目内容
【题目】“校园安全”越来越受到人们的关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．根据图中信息回答下列问题：
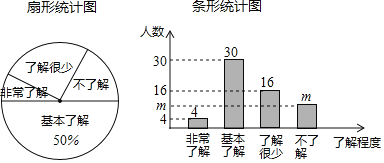
（1）接受问卷调查的学生共有______人，条形统计图中m的值为______；
（2）扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______；
（3）若该中学共有学生1800人，根据上述调查结果，可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人；
（4）若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛，请用列表或画树状图的方法，求恰好抽到1名男生和1名女生的概率．
【答案】（1）60，10；（2）96°；（3）1020；（4）
【解析】
(1)根据基本了解的人数以及所占的百分比可求得接受调查问卷的人数，进行求得不了解的人数，即可求得m的值；
(2)用360度乘以“了解很少”的比例即可得；
(3)用“非常了解”和“基本了解”的人数和除以接受问卷的人数，再乘以1800即可求得答案；
(4)画树状图表示出所有可能的情况数，再找出符合条件的情况数，利用概率公式进行求解即可.
(1)接受问卷调查的学生共有
(人)，
，
故答案为：60，10；
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数
，
故答案为：96°；
(3)该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为：
(人)，
故答案为：1020；
(4)由题意列树状图：
由树状图可知，所有等可能的结果有12种，恰好抽到1名男生和1名女生的结果有8种，
∴恰好抽到1名男生和1名女生的概率为
．
练习册系列答案
相关题目
