题目内容
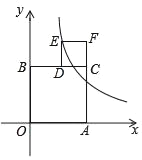
【题目】王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为z=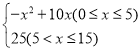 ,且用于回顾反思的时间不超过用于解题的时间.
,且用于回顾反思的时间不超过用于解题的时间.
(1)求王亮解题的学习收益量y与用于解题的时间x之间的函数关系式,并写出自变量x的取值范围;
(2)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?(学习收益总量=解题的学习收益量+回顾反思的学习收益量)
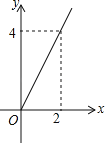
【答案】(1)y=2x. 自变量x的取值范围是:15≤x≤30;(2)解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.
【解析】
(1)设王亮解题的学习收益量y与用于解题的时间x之间的函数关系式为y=kx,观察图象可知该函数图象过点(2,4),代入即可求得k值,由此即可求得函数解析式,根据题意直接确定x的取值范围即可;(2)设王亮用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为W,分当0≤x≤5时和当5<x≤15时两种情况求得w与x的函数关系式,根据函数的性质求得w的最大值,比较即可解答.
解:(1)设y=kx,把(2,4)代入,
得:k=2,
∴y=2x.
自变量x的取值范围是:15≤x≤30.
(2)设王亮用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为W,
则他用于解题的时间为(30﹣x)分钟.
当0≤x≤5时,W=﹣x2+10x+2(30﹣x)=﹣x2+8x+60=﹣(x﹣4)2+76.
∴当x=4时,W最大=76.
当5<x≤15时,W=25+2(30﹣x)=﹣2x+85.
∵W随x的增大而减小,
∴当x=5时,W最大=75
综合所述,当x=4时,W最大=76,此时30﹣x=26.
即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.

 阅读快车系列答案
阅读快车系列答案