Question

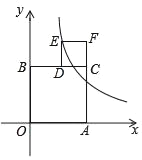
【题目】如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数（k＞0）在第一象限的图象经过点E，若正方形AOBC和正方形CDEF的面积之差为6，则k＝_____．

Answer 1

【答案】6

【解析】

设出正方形AOBC的边长为与正方形CDEF的边长，表示出E点，然后E点在反比例函数上，直接代入，利用面积直接解出k即可

解：设正方形AOBC的边长为a，正方形CDEF的边长为b，则E（a﹣b，a+b），

∵反比例函数的图象经过点E，

∴（a+b）（a﹣b）＝k，

整理为a2﹣b2＝k，

∵S正方形AOBC＝a2，S正方形CDEF＝b2，

∴S正方形AOBC﹣S正方形CDEF＝6，

即a2﹣b2＝6，

∴k＝6，

故答案为：6