题目内容
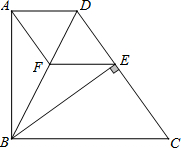
如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,EF是中位线,ED平分∠ADC,下面的结论:①CE平分∠BCD;②CD=AD+BC;③点E到CD的距离为
AB,其中正确结论的个数有( )

| 1 |
| 2 |
| A.0个 | B.1个 | C.2个 | D.3个 |

①正确:∵EF是梯形的中位线
∴EF∥AD∥BC,EF=
(AD+BC)
∵EF∥AD
∴∠ADE=∠DEF
∵ED平分∠ADC
∴∠DEF=∠EDF
∴EF=FD
∴EF=FC
∴∠FEC=∠FCE
∵EF∥BC
∴∠FEC=∠BCE
∴∠FCE=∠BCE
即CE平分∠BCD
②正确:由①中的证明得,EF=
(AD+BC),EF=FD=FC,∴CD=AD+BC;
③正确:根据角平分线的性质定理,得点E到CD的距离等于AE,即为
AB;
所以三个结论都正确,故选D.
∴EF∥AD∥BC,EF=
| 1 |
| 2 |
∵EF∥AD
∴∠ADE=∠DEF
∵ED平分∠ADC
∴∠DEF=∠EDF
∴EF=FD
∴EF=FC
∴∠FEC=∠FCE
∵EF∥BC
∴∠FEC=∠BCE
∴∠FCE=∠BCE
即CE平分∠BCD
②正确:由①中的证明得,EF=
| 1 |
| 2 |
③正确:根据角平分线的性质定理,得点E到CD的距离等于AE,即为
| 1 |
| 2 |
所以三个结论都正确,故选D.

练习册系列答案
相关题目



 出相应的t的值和P、Q的坐标;如不可能,请说明理由.
出相应的t的值和P、Q的坐标;如不可能,请说明理由.