Question

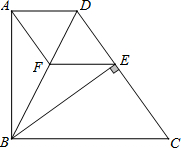
如图，在直角梯形ABCD中，AD∥BC，AB⊥AD，BC=CD，BE⊥CD，垂足为E，点F在BD上，连接AF、EF．
（1）求证：DA=DE；
（2）如果AF∥CD，求证：四边形ADEF是菱形．
（3）如果∠C=60°，EC=3，求AB的长．

Answer 1

证明：（1）∵BC=CD，
∴∠CDB=∠CBD，
∵AD∥BC，
∴∠ADB=∠CBD，
∴∠ADB=∠CDB，
又∵AB⊥AD，BE⊥CD，
∴∠BAD=∠BED=90°，
在△ABD和△EBD中，
∵

∠ADB=∠CDB ∠BAD=∠BED BD=BD

∴△ABD≌△EBD（AAS），
∴AD=ED．

（2）∵AF∥CD，∴∠AFD=∠EDF，
∴∠AFD=∠ADF，即得AF=AD，
又∵AD=ED，
∴AF=DE，
∴四边形ADEF是平行四边形，
又∵AD=ED，
∴四边形ADEF是菱形；

（3）∵∠C=60°，EC=3，tan60°=

BE

CE

=

3

，
∴BE=3

3

，
∵AB=BE，
∴AB=3

3

．