题目内容
【题目】阅读探索题:
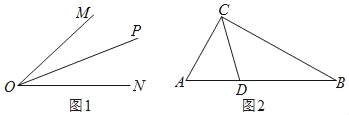
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
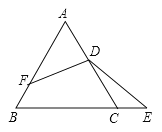
如图2,在 Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
【答案】(1)证明见解析(2)证明见解析
【解析】
1)根据以O为圆心任意长为半径作弧,交射线ON,OM为C,B两点,OP是∠MON的平分线,运用SAS判定△AOB≌△AOC即可;
(2)先截取CE=CA,连接DE,根据SAS判定△CAD≌△CED,得出AD=DE,∠A=∠CED=60°,AC=CE,进而得出结论BC=AC+AD;
(1)
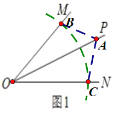
证明:在△AOB和△AOC中, 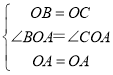
∴△AOB≌△AOC(SAS).
(2)
在CB上截取CE=CA,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△ECD中, 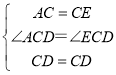
∴△ACD≌△ECD(SAS),
∴∠CAD=∠CED=60°,
∵∠ACB=90°,
∴∠B=30°,
∴∠EDB=30°,
即∠EDB=∠B,
∴DE=EB,
∵BC=CE+BE,
∴BC=AC+DE,
∴BC=AC+AD.

练习册系列答案
相关题目