Question

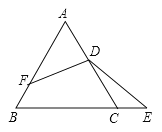
【题目】如图，△ABC是等边三角形，D是AC的中点，点E在BC的延长线上，点F在AB上，.若AB=5，则BE+BF的长度为（ ）

A.7.5B.8C.8.5D.9

Answer 1

【答案】A

【解析】

作DH∥BC交AB于H．通过证明△DHF≌△DCE，可证得HF＝CE即可推出BF＋BE＝BH＋BC，根据三角形中位线定理，可得BH＝AB，由AB=5，即可求得答案．

解：如图，作DH∥BC交AB于H．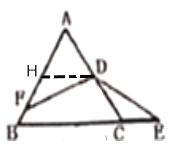

∵△ABC是等边三角形，
∴∠A＝∠B＝∠ACB＝60°，
∵DH∥BC，
∴∠AHD＝∠B＝60°，∠ADH＝∠ACB＝60°
∴△AHD是等边三角形，

∵D为AC的中点，

∴DH＝AD＝DC，∠DHF＝∠DCE＝∠HDC＝120°，
∵∠HDC＝∠FDE＝120°，
∴∠HDF＝∠CDE，
在△DHF和△DCE中，

∴△DHF≌△DCE（ASA），

∴HF＝CE，

∴BF＋BE＝BF＋HF＋BC＝BH＋BC，

∵△ABC为等边三角形，D为AC的中点，DH∥BC，AB=5，
∴BC＝5，BH＝AB＝×5＝，

∴BF＋BE＝＋5＝7.5．

故选：A．