题目内容
已知抛物线y=ax2+bx+c的顶点为A(3,-3),与x轴的一个交点为B(1,0).
(1)求抛物线的解析式.
(2)P是y轴上一个动点,求使P到A、B两点的距离之和最小的点P0的坐标.
(3)设抛物线与x轴的另一个交点为C.在抛物线上是否存在点M,使得△MBC的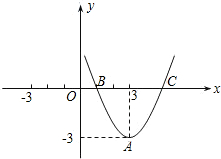 面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
(1)求抛物线的解析式.
(2)P是y轴上一个动点,求使P到A、B两点的距离之和最小的点P0的坐标.
(3)设抛物线与x轴的另一个交点为C.在抛物线上是否存在点M,使得△MBC的
 面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.(1)设抛物线的解析式为:y=a(x-3)2-3,依题意有:
a(1-3)2-3=0,a=
,
∴该抛物线的解析式为:y=
(x-3)2-3=
x2-
x+
.
(2)设B点关于y轴的对称点为B′,则B′(-1,0);
设直线AB′的解析式为y=kx+b,则有:
,
解得
;
∴y=-
x-
;
故P0(0,-
).
(3)由(1)的抛物线知:
y=
x2-
x+
=
(x-1)(x-5),
故C(5,0);
∵S四边形AP0BC=S△AB′C-S△BB′P0
=
×6×3-
×2×
=
;
∴S△BCM=
S四边形AP0BC=
;
易知BC=4,则|yM|=
;
当M的纵坐标为
时,
x2-
x+
=
,
解得x=3+
,x=3-
;
当M的纵坐标为-
时,
x2-
x+
=-
,
解得x=3+
,x=3-
;
故符合条件的M点有四个,它们的坐标分别是:
M1(3+
,
),M2(3-
,
),M3(3+
,-
),M4(3-
,-
).

a(1-3)2-3=0,a=
| 3 |
| 4 |
∴该抛物线的解析式为:y=
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
(2)设B点关于y轴的对称点为B′,则B′(-1,0);
设直线AB′的解析式为y=kx+b,则有:
|
解得
|
∴y=-
| 3 |
| 4 |
| 3 |
| 4 |
故P0(0,-
| 3 |
| 4 |
(3)由(1)的抛物线知:
y=
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
| 3 |
| 4 |
故C(5,0);
∵S四边形AP0BC=S△AB′C-S△BB′P0
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 33 |
| 4 |
∴S△BCM=
| 1 |
| 3 |
| 11 |
| 4 |
易知BC=4,则|yM|=
| 11 |
| 8 |
当M的纵坐标为
| 11 |
| 8 |
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
| 11 |
| 8 |
解得x=3+
| ||
| 6 |
| ||
| 6 |
当M的纵坐标为-
| 11 |
| 8 |
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
| 11 |
| 8 |
解得x=3+
| ||
| 6 |
| ||
| 6 |
故符合条件的M点有四个,它们的坐标分别是:
M1(3+
| ||
| 6 |
| 11 |
| 8 |
| ||
| 6 |
| 11 |
| 8 |
| ||
| 6 |
| 11 |
| 8 |
| ||
| 6 |
| 11 |
| 8 |


练习册系列答案
相关题目


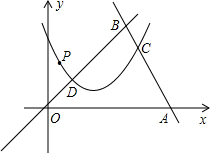 y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.
y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.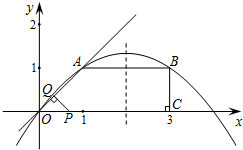

 开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.
开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.