题目内容
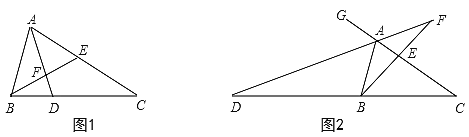
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
【答案】(1)证明见解析;(2)(1)中结论仍成立,理由见解析.
【解析】
(1)首先根据角平分线的性质可得∠BAD=∠DAC,再根据内角与外角的性质可得∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,进而得到∠EFD=∠ADC;
(2)首先根据角平分线的性质可得∠BAD=∠DAG,再根据等量代换可得∠FAE=∠BAD,然后再根据内角与外角的性质可得∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,进而得∠EFD=∠ADC.
(1)∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中结论仍成立;理由:
∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.

练习册系列答案
相关题目