��Ŀ����
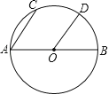
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����B��90����AB��8 cm��AD��12 cm��BC��18 cm����P�ӵ�A��������1 cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������2 cm/s���ٶ����B�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶���������������������������⣺
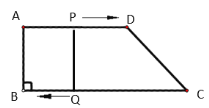
��1�����˶���ʼ����tȡ��ֵʱ���ı���PQBA�Ǿ��Σ�
��2���������˶��������Ƿ����tֵ��ʹ���ı���PQCD�����Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
��3���������˶��������Ƿ����t��ʹ����DQC�ǵ��������Σ������ڣ������tֵ���������ڣ���˵�����ɣ�
���𰸡���1��6����2�������ڣ����������������3�����ڣ���t��5��6��![]() ʱ����DQC�ǵ��������Σ�
ʱ����DQC�ǵ��������Σ�
��������
��1�������⣬��AP��t��DP��12��t��CQ��2t��BQ��18��2t���ٸ��ݾ��ε��ж����м��㼴�ɵõ��𰸣�
��2��Ҫʹ�ı���PQCD�����Σ����ı���PQCDһ����ƽ���ı��Σ�������֪��t��4ʱ���ı���PQCD��ƽ���ı��Σ���DP��12��t��8��10����DP��DC�����������ε��ж��õ��𰸣�
��3��������������ۣ��ٵ�QC��DCʱ����2t��10����t��5��
�ڵ�DQ��DCʱ������D��DH��CQ���ɹ��ɶ����õ�DC��10����t��6��
�۵�QD��QCʱ������D��DH��CQ����Rt��DQH�У�DH2��QH2��DQ2������õ�t��![]() ��
��
�⣺��1����ͼ�������⣬��AP��t��DP��12��t��CQ��2t��BQ��18��2t��
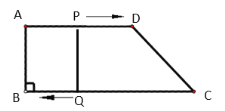
Ҫʹ�ı���PQBA�Ǿ��Σ�������B��90����AD��BC����AP��BQ��ֻ������AP��BQ����t��18��2t�����t��6��
���Ե�t��6ʱ���ı���PQBA�Ǿ��Σ�
��2�������ڣ����ɣ�
Ҫʹ�ı���PQCD�����Σ����ı���PQCDһ����ƽ���ı��Σ�
����֪��t��4ʱ���ı���PQCD��ƽ���ı��Σ�
��ʱDP��12��t��8��10����DP��DC��
������֪�ٶ��˶����ı���PQCDֻ����ƽ���ı��Σ��������������Σ�
��3����DQC�ǵ���������ʱ��������������ۣ�
����ͼ1����QC��DCʱ����2t��10����t��5��
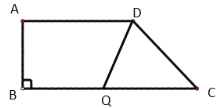
ͼ1
����ͼ2����DQ��DCʱ������D��DH��CQ��
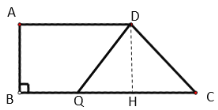
ͼ2
��QH��CH��![]() CQ��t��
CQ��t��
��Rt��DHC��DH��8��CH��BC��AD��6��
��DC��![]() ��10��
��10��
��t��6��
����ͼ3����QD��QCʱ������D��DH��CQ��
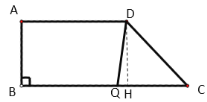
ͼ3
DH��8��CH��6��DC��10��CQ��QD��2t��QH��|2t��6|��
��Rt��DQH��DH2��QH2��DQ2��
��82��|2t��6|2��(2t)2��
���t��![]() ��
��
���ϣ���t��5��6��![]() ʱ����DQC�ǵ��������Σ�
ʱ����DQC�ǵ��������Σ�

����Ŀ��Ϊ�˽�ʮ�ߴ�����������ij��У�ʵ�ֿ�Խʽ��չ��������������������Ͷ�ʼƻ������ƽ������·������Ҫ������ʯ�����ƻ�ÿСʱ�ھ���ʯ��270m3���־�����ij���ͻ�е����˾���üס��������ͺŵ��ھ������������������˾�ṩ���ھ���й���Ϣ�����
��𣨵�λ��Ԫ/̨ʱ�� | �ھ���ʯ��������λ��m3/̨ʱ�� | |
�����ھ�� | 200 | 30 |
�����ھ�� | 260 | 40 |
��1�������üס��������ͺŵ��ھ����8̨��ǡ�����ÿСʱ���ھ�������ס��������ͺŵ��ھ���������̨��
��2�����ÿСʱ֧���������1780Ԫ����ǡ�����ÿСʱ���ھ�������ô���м��ֲ�ͬ�����÷�����