题目内容
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆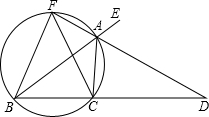 于点F,连接FB、FC.
于点F,连接FB、FC.(1)求证:FB=FC;
(2)求证:FB2=FA•FD;
(3)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6cm,求AD的长.
分析:(1)可通过证角相等来得出边相等,根据ACBF是圆的内接四边形,那么外角∠DAC=∠FBC,那么关键就是证明∠FCB=∠DAC,根据AD平分∠EAC,即∠EAD=∠DAC=∠FAB,我们发现∠FAB和∠FCB正好对应了同一段弧,因此便可得出∠FBC=∠FCB了;
(2)本题实际要证明△FBA和△FDB相似,(1)中已证得∠FAB=∠FCB=∠FBC,又有一个公共角,因此两三角形就相似了;
(3)根据∠EAC=120°可以得到∠DAC=60°,根据AB是△ABC外接圆的直径可以提出AC⊥BC,然后在直角三角形ABC中,有∠BAC的度数,有BC的长,就能求出AC的长,然后在直角三角形ACD中,根据∠ACD=60°,即可用三角函数求出AD.
(2)本题实际要证明△FBA和△FDB相似,(1)中已证得∠FAB=∠FCB=∠FBC,又有一个公共角,因此两三角形就相似了;
(3)根据∠EAC=120°可以得到∠DAC=60°,根据AB是△ABC外接圆的直径可以提出AC⊥BC,然后在直角三角形ABC中,有∠BAC的度数,有BC的长,就能求出AC的长,然后在直角三角形ACD中,根据∠ACD=60°,即可用三角函数求出AD.
解答:(1)证明:∵AD平分∠EAC,
∴∠EAD=∠DAC,
∵四边形AFBC内接于圆,
∴∠DAC=∠FBC,
∵∠EAD=∠FAB=∠FCB,
∴∠FBC=∠FCB,
∴FB=FC;
(2)证明:∵∠FAB=∠FCB=∠FBC,∠AFB=∠BFD
∴△FBA∽△FDB,
∴
=
,
∴FB2=FA•FD;
(3)解:∵AB是圆的直径,
∴∠ACB=90°
∵∠EAC=120°,
∴∠DAC=
∠EAC=60°,
∵四边形ACBF内接于圆,
∴∠DAC=∠FBC=60°,又FB=FC,
∴△BFC是等边三角形,
∴∠BAC=∠BFC=60°,
∴∠D=30°,
∵BC=6,
∴AC=2
,
∴AD=2AC=4
.
∴∠EAD=∠DAC,
∵四边形AFBC内接于圆,
∴∠DAC=∠FBC,
∵∠EAD=∠FAB=∠FCB,
∴∠FBC=∠FCB,
∴FB=FC;
(2)证明:∵∠FAB=∠FCB=∠FBC,∠AFB=∠BFD
∴△FBA∽△FDB,
∴
| FB |
| FD |
| FA |
| FB |
∴FB2=FA•FD;
(3)解:∵AB是圆的直径,
∴∠ACB=90°
∵∠EAC=120°,
∴∠DAC=
| 1 |
| 2 |
∵四边形ACBF内接于圆,
∴∠DAC=∠FBC=60°,又FB=FC,
∴△BFC是等边三角形,
∴∠BAC=∠BFC=60°,
∴∠D=30°,
∵BC=6,
∴AC=2
| 3 |
∴AD=2AC=4
| 3 |
点评:本题主要的考查了圆周角定理,相似三角形的判定和性质,根据圆周角定理和圆的内接四边形得出角相等是解题的关键,综合性较强,对学生的要求比较高.

练习册系列答案
相关题目
 9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( )
9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( )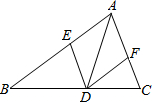 18、如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:
18、如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是: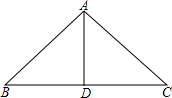 如图,已知AD是等腰三角形ABC底边上的高,AD与底边BC的比是2:3,等腰三角形的面积是12cm,求等腰三角形ABC的周长.
如图,已知AD是等腰三角形ABC底边上的高,AD与底边BC的比是2:3,等腰三角形的面积是12cm,求等腰三角形ABC的周长.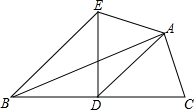 如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm. 如图,已知AD是△ABC的角平分线,DE∥AB交AC于点E.那么△ADE是等腰三角形吗?请说明理由.
如图,已知AD是△ABC的角平分线,DE∥AB交AC于点E.那么△ADE是等腰三角形吗?请说明理由.