题目内容
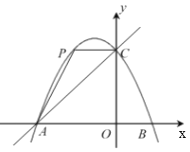
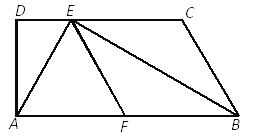
【题目】如图，已知梯形ABCD中，AB∥CD，∠D=90°，BE平分∠ABC，交CD于点E，F是AB的中点，联结AE、EF，且AE⊥BE．
求证：（1）四边形BCEF是菱形；
（2）
.
【答案】（1）证明见解析；（2）证明见解析.
【解析】分析：（1）根据角平分线的性质可得出∠ABE=∠CBE，由直角三角形斜边上中线等于斜边的一半可得出EF=BF=
AB，进而可得出∠FEB=∠FBE=∠CBE，由“内错角相等，两直线平行”可得出EF∥BC，结合AB∥CD可得出四边形BCEF是平行四边形，再由邻边EF=BF即可证出四边形BCEF是菱形；
（2）根据菱形的性质可得出BC=BF，结合BF=AB可得出AB=2BC，由AB∥CD可得出∠DEA=∠EAB，结合∠D=∠AEB=90°可证出△EDA∽△AEB，根据相似三角形的性质可得出BEAE=ADBA，代入BA=2BC即可证出结论．
详解：（1）∵BE平分∠ABC，∴∠ABE=∠CBE．
∵AE⊥BE，∴∠AEB=90°．
∵F是AB的中点，∴EF=BF=AB，∴∠FEB=∠FBE=∠CBE，∴EF∥BC．
∵AB∥CD，∴四边形BCEF是平行四边形．
∵EF=BF，∴四边形BCEF是菱形．
（2）∵四边形BCEF是菱形，∴BC=BF．
∵BF=AB，∴AB=2BC．
∵AB∥CD，∴∠DEA=∠EAB．
∵∠D=∠AEB=90°，∴△EDA∽△AEB，∴
=
，∴BEAE=ADBA，∴BEAE=2ADBC．
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A. 抛物线于x轴的一个交点坐标为（﹣2，0）
B. 抛物线与y轴的交点坐标为（0，6）
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
【题目】按下图方式摆放餐桌和椅子，
…
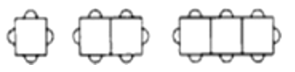（1）1张长方形餐桌可坐4人，2张长方形餐桌拼在一起可坐______人．
（2）按照上图的方式继续排列餐桌，完成下表．
桌子张数 | 3 | 4 | 5 | n |
可坐人数 | ______ | ______ | ______ | ______ |
（3）一家餐厅有40张这样的长方形餐桌，某用餐单位要求餐厅按照上图方式，每8张长方形餐桌拼成1张大桌子，则该餐厅此时能容纳多少人用餐？
