题目内容
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转90°得到P′,连CP′,则线段CP′的最小值为 . 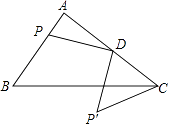
【答案】2
【解析】解:如图所示,过P'作P'E⊥AC于E,
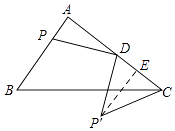
则∠A=∠P'ED=90°,
由旋转可得,DP=P'D,∠PDP'=90°,
∴∠ADP=∠EP'D,
在△DAP和△P'ED中,
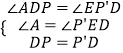 ,
,
∴△DAP≌△P'ED(AAS),
∴P'E=AD=2,
∴当AP=DE=2时,DE=DC,即点E与点C重合,
此时CP'=EP'=2,
∴线段CP′的最小值为2,
所以答案是:2.
【考点精析】通过灵活运用点到直线的距离和旋转的性质,掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

练习册系列答案
相关题目