题目内容
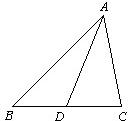 18、如图,已知:AD是△ABC的中线,AB>AC,求证:∠CAD>∠BAD.
18、如图,已知:AD是△ABC的中线,AB>AC,求证:∠CAD>∠BAD.分析:把△ABD绕点D顺时针旋转180°到△ECD的位置,根据旋转的性质得∠E=∠BAD,CE=AB,而AB>AC,得CE>AC,根据三角形的边角关系得到∠CAD>∠E,从而得到结论.
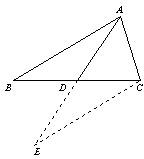
解答:解:把△ABD绕点D顺时针旋转180°到△ECD的位置,如图,
∴∠E=∠BAD,CE=AB
而AB>AC,
∴CE>AC,
∴∠CAD>∠E,
所以∠CAD>∠BAD.
∴∠E=∠BAD,CE=AB
而AB>AC,
∴CE>AC,
∴∠CAD>∠E,
所以∠CAD>∠BAD.

点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了三角形的边角关系:大边对大角.

练习册系列答案
相关题目

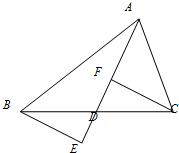 23、如图,已知:AD是BC上的中线,E点在AD延长线上,且DF=DE.
23、如图,已知:AD是BC上的中线,E点在AD延长线上,且DF=DE.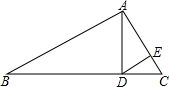 如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△CDE=a,那么S△ABC等于( )
如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△CDE=a,那么S△ABC等于( ) 如图,已知:AD是⊙O的直径,AB、AC是弦,且AB=AC.
如图,已知:AD是⊙O的直径,AB、AC是弦,且AB=AC.
 如图,已知:AD是BC上的中线,BE⊥AD于点E,且DF=DE.求证:CF⊥AD.
如图,已知:AD是BC上的中线,BE⊥AD于点E,且DF=DE.求证:CF⊥AD.