题目内容
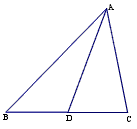
26、如图,已知线段AD是△ABC的中线,且AB=6,AD=4,AC边长为奇数.求边AC的长.

分析:此题需延长AD至E,使DE=AD,连接BE.构造全等三角形,把要求的线段和已知的线段构造到一个三角形中,根据三角形的三边关系求得AC的取值范围,再根据奇数这一条件求得AC的值.
解答: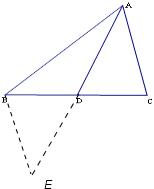 解:延长AD至E,使DE=AD,连接BE.
解:延长AD至E,使DE=AD,连接BE.
∵AD=DE,∠ADC=∠BDE,AC=BE,
∴△ACD≌△EBD.
∴BE=AC.
又AB=6,AE=8,
根据三角形的三边关系,得
2<AC<14.
又AC是奇数,
则AC长为:3、5、7、9、11、13.
 解:延长AD至E,使DE=AD,连接BE.
解:延长AD至E,使DE=AD,连接BE.∵AD=DE,∠ADC=∠BDE,AC=BE,
∴△ACD≌△EBD.
∴BE=AC.
又AB=6,AE=8,
根据三角形的三边关系,得
2<AC<14.
又AC是奇数,
则AC长为:3、5、7、9、11、13.
点评:此题中常见的辅助线:倍长中线.综合运用了全等三角形的判定和性质以及三角形的三边关系.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 9、如图,已知:AD是△ABC的中线.
9、如图,已知:AD是△ABC的中线.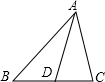 如图,已知线段AD是△ABC的中线,且AB=6,AD=4,AC边长为奇数.求边AC的长.
如图,已知线段AD是△ABC的中线,且AB=6,AD=4,AC边长为奇数.求边AC的长.