题目内容
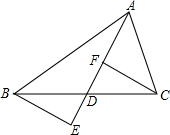如图，已知：AD是BC上的中线，BE⊥AD于点E，且DF=DE．求证：CF⊥AD．分析：由中线的想可以得出BD=CD，再由SAS就可以得出△BDE≌△CDF，就可以得出结论．
解答：证明：∵AD是BC上的中线，
∴BD=CD．
∵BE⊥AD，
∴∠E=90°．
在△BDE和△CDF中
，
∴△BDE≌△CDF（SAS），
∴∠E=∠CFD=90°，
∴CF⊥AD．
∴BD=CD．
∵BE⊥AD，
∴∠E=90°．
在△BDE和△CDF中
|
∴△BDE≌△CDF（SAS），
∴∠E=∠CFD=90°，
∴CF⊥AD．
点评：本题考查了中线的性质的运用，全扥三角形的判定与性质的运用，垂直的判定的运用，解答时证明三角形全等是关键．
练习册系列答案
相关题目
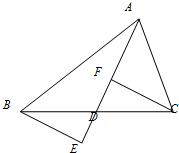23、如图，已知：AD是BC上的中线，E点在AD延长线上，且DF=DE．
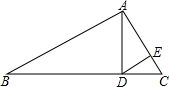如图，已知：AD是Rt△ABC斜边BC上的高线，DE是Rt△ADC斜边AC上的高线，如果DC：AD=1：2，S△CDE=a，那么S△ABC等于（ ）
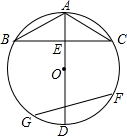如图，已知：AD是⊙O的直径，AB、AC是弦，且AB=AC．