题目内容
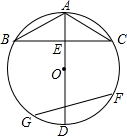 如图,已知:AD是⊙O的直径,AB、AC是弦,且AB=AC.
如图,已知:AD是⊙O的直径,AB、AC是弦,且AB=AC.(1)求证:直径AD平分∠BAC;
(2)若BC经过半径OA的中点E,F是
 |
| CD |
 |
| FB |
分析:(1)根据全等或等腰三角形的性质即可得出AO⊥BC,AO平分BC.
(2)求出∠AOC的度数,求出弧AC度数,分别求出弧CD、弧CF、弧DF、弧BF、弧GF的度数,求出∠GOF=90°,根据勾股定理求出即可.
(2)求出∠AOC的度数,求出弧AC度数,分别求出弧CD、弧CF、弧DF、弧BF、弧GF的度数,求出∠GOF=90°,根据勾股定理求出即可.
解答:(1)证明:连接OB,OC,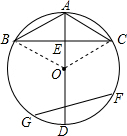
∵在△ABO和△ACO中,
∴△ABO≌△ACO,
∴∠BAO=∠CAO,
∴直径AD平分∠BAC;
(2)解:连接OG、OF,OC,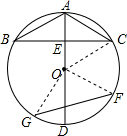
∵BC过AO中点,
∴AE=OE=
OA=
OC,
∵AO⊥BC,
∴∠OEC=90°,
∴∠OCE=30°,
∴∠AOC=60°,
即弧AC度数是60°,
∵AD为直径,
∴弧CD的度数是180°-60°=120°,
∵F为弧CD中点,
∴弧CF的度数和弧DF的度数都等于60°,
∵AO⊥BC,AO平分BC,
∴弧BD的度数=弧CD的度数,是120°,
∴弧BDF的度数是120°+60°=180°,
∵G为弧BDF的中点,
∴弧GF度数是90°,
∴∠GOF=90°,
∵OG=OF=1,
∴由勾股定理得:GF=
=
.

∵在△ABO和△ACO中,
|
∴△ABO≌△ACO,
∴∠BAO=∠CAO,
∴直径AD平分∠BAC;
(2)解:连接OG、OF,OC,

∵BC过AO中点,
∴AE=OE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AO⊥BC,
∴∠OEC=90°,
∴∠OCE=30°,
∴∠AOC=60°,
即弧AC度数是60°,
∵AD为直径,
∴弧CD的度数是180°-60°=120°,
∵F为弧CD中点,
∴弧CF的度数和弧DF的度数都等于60°,
∵AO⊥BC,AO平分BC,
∴弧BD的度数=弧CD的度数,是120°,
∴弧BDF的度数是120°+60°=180°,
∵G为弧BDF的中点,
∴弧GF度数是90°,
∴∠GOF=90°,
∵OG=OF=1,
∴由勾股定理得:GF=
| 12+12 |
| 2 |
点评:本题考查了垂径定理,勾股定理,全等三角形的性质和判定,等腰三角形的性质的应用,主要考查学生综合运用定理进行推理的能力.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目

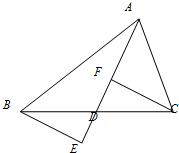 23、如图,已知:AD是BC上的中线,E点在AD延长线上,且DF=DE.
23、如图,已知:AD是BC上的中线,E点在AD延长线上,且DF=DE.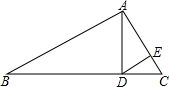 如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△CDE=a,那么S△ABC等于( )
如图,已知:AD是Rt△ABC斜边BC上的高线,DE是Rt△ADC斜边AC上的高线,如果DC:AD=1:2,S△CDE=a,那么S△ABC等于( )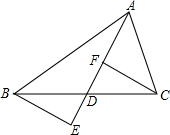 如图,已知:AD是BC上的中线,BE⊥AD于点E,且DF=DE.求证:CF⊥AD.
如图,已知:AD是BC上的中线,BE⊥AD于点E,且DF=DE.求证:CF⊥AD.