题目内容
如图,已知直线l经过点A(1,0),与双曲线y=(x>0)交于点B(2,1).过点P(a,a-1)
(a>1)作x轴的平行线分别交双曲线y=(x>0)和y=-(x<0)于点M、N.
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA.
(a>1)作x轴的平行线分别交双曲线y=(x>0)和y=-(x<0)于点M、N.
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA.

解:(1)由点B(2,1)在y=上,有2=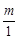 ,即m=2。
,即m=2。
设直线l的解析式为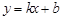 ,由点A(1,0),点B(2,1)在
,由点A(1,0),点B(2,1)在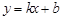 上,得
上,得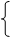 , ,解之,得
, ,解之,得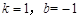
∴所求直线l的解析式为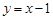 。
。
(2)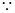 点P(a,a-1)(a>1)在直线y=2上, ∴P(3,2)
点P(a,a-1)(a>1)在直线y=2上, ∴P(3,2)
∴ P在直线l上,是直线y=2和l的交点,
∴根据条件得各点坐标为N(-1,2),M(1,2),P(3,2)。
∴NP=3-(-1)=4,MP=3-1=2,
AP=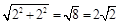 , BP=
, BP=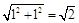
∴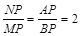
在△PMB和△PNA中,∠MPB=∠NPA
∴ △PMB∽△PNA。
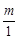 ,即m=2。
,即m=2。
|
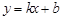 ,由点A(1,0),点B(2,1)在
,由点A(1,0),点B(2,1)在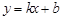 上,得
上,得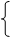 , ,解之,得
, ,解之,得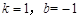
∴所求直线l的解析式为
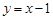 。
。 (2)
 点P(a,a-1)(a>1)在直线y=2上, ∴P(3,2)
点P(a,a-1)(a>1)在直线y=2上, ∴P(3,2)∴ P在直线l上,是直线y=2和l的交点,
∴根据条件得各点坐标为N(-1,2),M(1,2),P(3,2)。
∴NP=3-(-1)=4,MP=3-1=2,
AP=
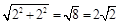 , BP=
, BP=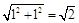
∴
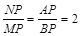
在△PMB和△PNA中,∠MPB=∠NPA
∴ △PMB∽△PNA。
(1)把点B坐标代入反比例函数,即可得m的值,把点A、B的坐标代入一次函数解析式,用待定系数法可求得直线解析式;
(2)两条对应边对应成比例,并且这两条边的夹角相等,可以判定两个三角形相似。
(2)两条对应边对应成比例,并且这两条边的夹角相等,可以判定两个三角形相似。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
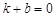
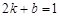
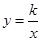 与一次函数
与一次函数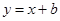 的图象在第一象限相交于点
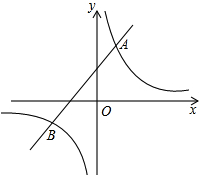
的图象在第一象限相交于点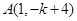 .
.
 与一次函数y=-x+2的图象交于A、B两点,且点A的横坐标是-2.
与一次函数y=-x+2的图象交于A、B两点,且点A的横坐标是-2.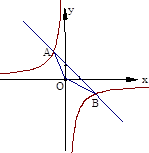
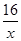 (x>0)的图象上,
(x>0)的图象上,
 的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
 的图象与一次函数y=2x+1的图象的一个交点是(1,k),则反比例函数的解析式是 ▲ .
的图象与一次函数y=2x+1的图象的一个交点是(1,k),则反比例函数的解析式是 ▲ . 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点 在第二象限;
在第二象限; ,并写出点
,并写出点
 的图象交于点
的图象交于点