题目内容
如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数 的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
(1)求反比例函数 和直线OE的函数解析式;
和直线OE的函数解析式;
(2)求四边形OAFC的面积.
 的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.(1)求反比例函数
 和直线OE的函数解析式;
和直线OE的函数解析式;(2)求四边形OAFC的面积.

解:(1)依题意,得点B的坐标为(3,4),点D的坐标为(3,2)
将(3,2)代入 ,得k=6.
,得k=6.
所以反比例函数的解析式为 .
.
设点E的坐标为(m,4),将其代入 ,m=
,m=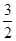 ,
,
故点E的坐标为(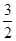 ,4).
,4).
设直线OE的解析式为 ,将(
,将(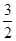 ,4)代入得
,4)代入得
所以直线OE的解析式为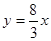 .
.
(2)连结AC,由勾股定理得 .
.
又∵ ,
,
∴ 由勾股定理的逆定理得∠CAF=90°.
∴ 。
。
将(3,2)代入
 ,得k=6.
,得k=6.所以反比例函数的解析式为
 .
. 设点E的坐标为(m,4),将其代入
 ,m=
,m=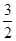 ,
,故点E的坐标为(
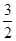 ,4).
,4). 设直线OE的解析式为
 ,将(
,将(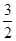 ,4)代入得
,4)代入得
所以直线OE的解析式为
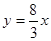 .
. (2)连结AC,由勾股定理得
 .
.又∵
 ,
,∴ 由勾股定理的逆定理得∠CAF=90°.
∴
 。
。(1)根据反比例图像上点D的坐标易求反比例函数的关系式;由于直线OE是一条过原点的直线,只要知道点E的坐标,而易得到点E的纵坐标且点E又在反比例函数 上,易求点E的横坐标。
上,易求点E的横坐标。
(2)利用转化思想,将不规则四边形转化成两个直角三角形,其中 是直角三角形需要利用勾股定理逆定理判断。
是直角三角形需要利用勾股定理逆定理判断。
 上,易求点E的横坐标。
上,易求点E的横坐标。(2)利用转化思想,将不规则四边形转化成两个直角三角形,其中
 是直角三角形需要利用勾股定理逆定理判断。
是直角三角形需要利用勾股定理逆定理判断。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

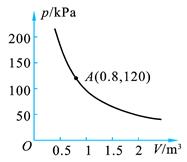
 的图象经过点(-1,2),k的值是
的图象经过点(-1,2),k的值是

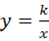 (k>0)经过A,E两点,若平行四边形AOBC的面积为24,则k= .
(k>0)经过A,E两点,若平行四边形AOBC的面积为24,则k= .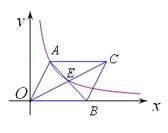
 轴和
轴和 轴,建立如图所示的平面直角坐标系.E是边AC上的一个动点(不与A,C重合),过E点的反比例函数
轴,建立如图所示的平面直角坐标系.E是边AC上的一个动点(不与A,C重合),过E点的反比例函数 的图象与BC边交于点F.
的图象与BC边交于点F. 问当点E运动到什么位置时,S有最大值,其最大值为多少?
问当点E运动到什么位置时,S有最大值,其最大值为多少?
 的图象与反比例函数
的图象与反比例函数 的图象相交于点(1,2),则
的图象相交于点(1,2),则
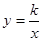 (
(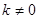 )的图像经过点
)的图像经过点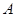 (-3,2),那么
(-3,2),那么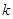 = .
= . 的图象经过点
的图象经过点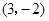 ,则
,则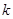 的值是( )
的值是( ) 

