Question

【题目】如图，直线AB：y=3x+3交x轴于点A；直线y=-x平移后经过点B，交x轴于点C（7，0），另一直线y=kx-k交x轴于点D，交直线BC于点E，连接DB，BD⊥x轴．

（1）求直线BC的解析式和点B的坐标；

（2）若直线DE将△BDC的面积分为1：2的两部分，求k的值．

Answer 1

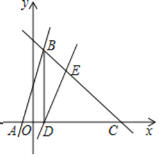
【答案】(1) y=-x+7, B（1，6）;(2)2.

【解析】

（1）根据函数图象的平移“左加右减”即可解答

（2）点BD⊥x轴，即可得出点B的纵坐标为△BDC的高，只要求出点E，点D的坐标即可求出k值．

依题意，（1）由图解的平移可得直线BC的解析式为：y=-x+7,

∵直线AB与直线BC交于点B，有，

解得，故点B的坐标为（1，6）；

（2）由（1）得点B的坐标为（1，6），

∵BD⊥x轴，且点D在x轴上，

∴点D的坐标为（1，0），

∴|DC|=7-1=6，

∴，

∵直线DE将△BDC的面积分成1：2，

∴S△DEC：S△DBC=2：3，

∴，

∴在△DEC中有，过点E作EF⊥x轴，

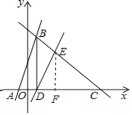
即EF为△DEC的高，

有，解得，EF=4，

又∵点E在直线BC上，将4代入y=-x+7得4=-x+7，

解得x=3，故点E的坐标为（3，4），

设直线DE的解析式为：y=kx+b，将点E，点D代入得，

解得，

故k的值为2．