题目内容
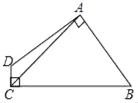
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.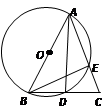
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90° 即AD是底边BC上的高.
又∵AB=AC,
∴△ABC是等腰三角形,
∴D是BC的中点
(2)证明:∵∠CBE与∠CAD是同弧所对的圆周角,
∴ ∠CBE=∠CAD.
又∵∠BCE=∠ACD,
∴△BEC∽△ADC;
(3)证明:由△BEC∽△ADC得: ![]() , 即CD·BC=AC·CE.
, 即CD·BC=AC·CE.
∵D是BC的中点,
∴CD= BC.
又∵AB=AC,∴CD·BC=AC·CE= ![]() BC ·BC=AB·CE 即BC
BC ·BC=AB·CE 即BC ![]() =2AB·CE=12
=2AB·CE=12
∴AB=6
∴⊙O的半径为3
【解析】(1)由AB是⊙O的直径,证出AD是底边BC上的高.根据等腰三角形三线合一的性质得出结论。
(2)根据同弧所对的圆周角相等,得出∠CBE=∠CAD,再根据两组角对应相等的两三角形相似。
(3)由△BEC∽△ADC得出对应边成比例,即可求出圆的半径。
【考点精析】本题主要考查了等腰三角形的性质和圆周角定理的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
相关题目