题目内容
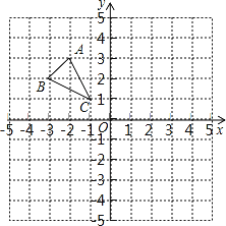
【题目】平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(2,7) ,直线l经过A点且平行于x
轴,直线l上的动点C从A点出发以每秒4个单位的速度沿直线l运动.若在x轴上有两点D、E,
连接DB、OB,连接EC、OC,满足DB=OB,EC=OC,设点C运动时间t秒,
(1) 如图1,若动点C从A点出发向左运动,当t=1秒时,
①求线段BC的长和点E的坐标;
②求此时DE与AC的数量关系?
(2)探究:动点C在直线l运动,无论t取何值,是否都存在上述(1)②中的数量关系? 若存在,请证明;若不存在,请说明理由.


图1 图2
【答案】(1) ①BC=5, E(-4,0)②DE=2AC (2)存在,证明见解析
【解析】试题分析:(1)①根据题意可知AC=4,AB=3,由勾股定理即可得BC的长,再根据EC=OC以及点C的坐标即可得点E的坐标;
②由点B的坐标以及DB=OB即可得点D的坐标,从而得到DE的长,从而可得;
(2)由题意可知AC=4t,C(2-4t,4),从而可得E(4-8t,0),由D(4,0)可得DE=8t,从而可得.
试题解析:(1)①当t=1时,AC=4t=4,4-2=2,所以C(-2,4),
由A(2,4)、B(2,7)可得AB=3,
由勾股定理则有BC=5,
因为EC=OC,C(-2,4),O(0,0),所以E(-4,0);
②由OB=BD,O(0,0),B(2,7),所以D(4,0),
由E(-4,0),所以DE=8,
因为AC=4,所以DE=2AC;
(2)存在,理由如下:
∵AC=4t,A(2,4),∴C(2-4t,4),
∵EC=OC, O(0,0),∴E(4-8t,0);
∵OB=BD,O(0,0),B(2,7),∴D(4,0),
∴DE=8t,
∴DE=2AC.

练习册系列答案
相关题目