��Ŀ����
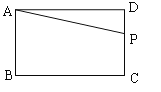
����Ŀ����ͼ1����֪������ABCD��AB=CD�� BC=AD��PΪ������ABCD���ϵĶ���������P��A����������A��B��C��D�˶���D��ֹͣ���ٶ�Ϊ2cm/s�����P�õ�ʱ��Ϊx������APD�����Ϊy![]() ��y��x�Ĺ�ϵ��ͼ2��ʾ.
��y��x�Ĺ�ϵ��ͼ2��ʾ.

��1��AB=________cm, BC=______cm;
��2��д��![]() ʱ,y��x֮��Ĺ�ϵʽ��
ʱ,y��x֮��Ĺ�ϵʽ��
��3����y=12ʱ����x��ֵ��
��4����P���߶�BC���˶�ʱ���Ƿ���ڵ�Pʹ����APD���ܳ���С�������ڣ������ʱ��APD�Ķ������������ڣ���˵�����ɣ�
���𰸡���1��AB=6cm��BC=12cm����2��y=12x����3��x=1��11����4�����ڣ���ʱ��APD =90��
����������1�����ݺ���ͼ��ɵô�A��B������3�룬��B��C����6�룬�ٶ�Ϊ2cm/s,��ɼ����AB��BC�ij��ȣ�
��2���������������ʽ�ɵ�: ����APD�����=![]() ��AP��2x�ɵó�y��x֮��Ĺ�ϵʽ��
��AP��2x�ɵó�y��x֮��Ĺ�ϵʽ��
��3����������ۣ�����P��AB��CD��ʱ�����x��ֵ����;
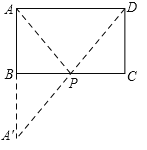
��4����A����ֱ��BC�ĶԳƵ�A�䣬����A��D��BC���ڵ�P����������֮�ʹ��ڵ����߿�֪A��D��С������APD���ܳ���С�������APD=��A��+��BAP=90�㣮
��1�����ɺ���ͼ��ɵã���P��A��B������3�룬��B��C����6�룬��P���ٶ�Ϊ2cm/s
��AB=6cm, BC=12cm;
��2����ͼ��ʾ��
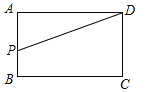
��![]() ʱ,��P���߶�AB�ϣ�AP��2x,
ʱ,��P���߶�AB�ϣ�AP��2x,
��S��ADP=![]() .
.
��3����ͼ��ʾ��
�����������
�ٵ�P��AB��ʱ����ͼ��ʾ����y=3ʱ��3=3x��x=1��

�ڵ�P��CD��ʱ����ͼ��ʾ����AB+BC+CP=t��
��PD=3+3+6-t=12-t��
��y=![]() PDAD=
PDAD=![]() ��6����12-t��=3��12-t����
��6����12-t��=3��12-t����
��y=3ʱ��3=3��12-t����
t=11��
������������y=3ʱ��x��ֵ��1���11�룻
��4�����ڣ���ͼ��ʾ���ӳ�AB��A�䣬ʹAB=A��B������A��D����BC��P������AP��
��ʱ��APD���ܳ���С��
��AA��=AB+BA��=3+3=6��
��AD=AA��=6��
���A��AD�ǵ���ֱ�������Σ�
���A��=45�㣬
�ߡ�ABC=90�㣬
��BP��AA����д��ߣ�
��AP=PA�䣬
���A��=��BAP=45�㣬
���APD=��A��+��BAP=90�㣮

 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�