题目内容
【题目】如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.

【答案】(1)证明见解析;
(2)150°.
【解析】试题分析:
(1)结合等边三角形和正方形的性质,用SAS证明△ABE≌△DCE;
(2)由∠ABE=90°-60°=30°,BA=BE得∠AEB的度数,同理得∠CDE的度数,即可求解.
试题解析:
(1)∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
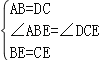 ,
,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,∴∠BAE=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵∠BAD=90°,∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.

练习册系列答案
相关题目
【题目】为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或八年级同学提一条合理化建议: .