题目内容
【题目】请先仔细阅读下列要求,然后解答相关问题.
(1)请补全以下求一元二次不等式-2x2-4x≥0的解集的过程;
①构造函数,画出图象:根据不等式特征构造二次函数y=-2x2-4x;并在平面直角坐标系中(如图)画出二次函数y=-2x2-4x的图象(只画出草图即可);
②求得界点,标示所需:当y=0时,求得方程-2x2-4x=0的解为 ;不等式-2x2-4x≥0的解集即为函数值y≥0时所对应的自变量x的取值范围;
③借助图象,写出解集;由所标示图象,可得不等式-2x2-4x≥0的解集为 ;
(2)请你利用(1)中求不等式解集的方法和步骤,①直接写出一元二次不等式x2-6x+3<10的解集为 ;
②直接写出一元二次不等式x2+3x>-1的解集为 .
解:如图所示.
【答案】(1) ①作图见解析; ②x1=0,x2=-2; ③-2≤x≤0; (2) ①-1<x<7; ②x<![]() 或x>
或x>![]() .
.
【解析】试题分析: ![]() ①利用描点法,作出函数的图象;
①利用描点法,作出函数的图象;
②当![]() 时,解方程求得
时,解方程求得![]() 的值,当
的值,当![]() 时,就是函数图象在
时,就是函数图象在![]() 轴上方的部分,据此即可解得;
轴上方的部分,据此即可解得;
③![]()
![]() ①仿照上边的例子,首先作出函数
①仿照上边的例子,首先作出函数![]() 的图象,然后求得当
的图象,然后求得当![]() 时对应的
时对应的![]() 的值,根据图象即可求解.
的值,根据图象即可求解.
②根据①的方法直接写出来.
试题解析: ![]() 图象如图所示:
图象如图所示:
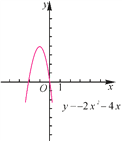
②令![]() ,
,
解得: ![]()
③由图象可以看出不等式![]() 的解集为:
的解集为: ![]()
![]() ①
①![]()
②![]() 或
或![]()

练习册系列答案
相关题目

