题目内容
【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点. ∠APC=∠CPB=60°.
(1)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积.

【答案】(1) PA+PB=PC;(2) ![]() .
.
【解析】试题分析:(1)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得;
(2)过点P作PE⊥AB,垂足为E,过点C作CF⊥AB,垂足为F,把四边形的面积转化为两个三角形的面积进行计算,当点P为![]() 的中点时,PE+CF=PC从而得出最大面积.
的中点时,PE+CF=PC从而得出最大面积.
试题解析:(1)在PC上截取PD=AP,如图,
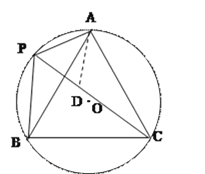
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴PC=BP+AP.
(2)当点P为![]() 的中点时,四边形APBC的面积最大.
的中点时,四边形APBC的面积最大.
理由如下,如图,过点P作PE⊥AB,垂足为E.
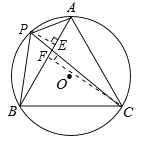
过点C作CF⊥AB,垂足为F.
∵S△APB=![]() ABPE,S△ABC=
ABPE,S△ABC=![]() ABCF,
ABCF,
∴S四边形APBC=![]() AB(PE+CF),
AB(PE+CF),
当点P为![]() 的中点时,PE+CF=PC,PC为⊙O的直径,
的中点时,PE+CF=PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
又∵⊙O的半径为1,
∴其内接正三角形的边长AB=![]() ,
,
∴S四边形APBC=![]() ×2×
×2×![]() =
=![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目


