题目内容
【题目】在平面直角坐标系中，点A、B在坐标轴上，其中A(0，
)、B(
，0)满足：
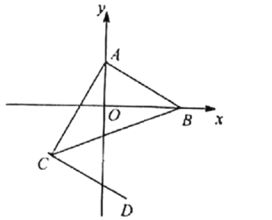
（1）求A、B两点的坐标；
（2）将线段AB平移到CD，点A的对应点为C(-2，t)，如图(1)所示．若三角形ABC的面积为9，求点D的坐标．
【答案】（1）A、B两点的坐标分别为(0，2)，(3，0)；（2）点D的坐标是（1，
）
【解析】
（1）利用非负数的性质结合二元一次方程组即可解决问题；
（2）根据补形法以及A、B、C三点坐标表示出△ABC的面积，再由三角形ABC的面积为9得出方程，解得点C坐标，由平移性质可得点D坐标.
解：（1）∵|2a-b-1|+
，
又∵|2a-b-1|≥0，
，
∴
，
解得：
，
∴A（0，2），B（3，0）；
（2）由题意得:∵A（0，2），B（3，0），C（-2，t），
根据补形法，
S△ABC=9=5（2-t）-
×2×（2-t）-×5×（-t）-×2×3，
解得：t=
，可得C（-2，），
将点C向下平移2个单位，向右平移3个单位得到点D，
∴D（1，）.
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
